SOLUTION: find the distance between (1,-3) and (-2,6). express as a radical or a number rounded to the nearest hundredth.

Algebra ->  Radicals -> SOLUTION: find the distance between (1,-3) and (-2,6). express as a radical or a number rounded to the nearest hundredth.      Log On


   

Question 743473: find the distance between (1,-3) and (-2,6). express as a radical or a number rounded to the nearest hundredth.
Answer by jim_thompson5910(35256) About Me  (Show Source):
You can put this solution on YOUR website!
Solved by pluggable solver: Distance Formula


The first point is (x1,y1). The second point is (x2,y2)


Since the first point is (1, -3), we can say (x1, y1) = (1, -3)
So x%5B1%5D+=+1, y%5B1%5D+=+-3


Since the second point is (-2, 6), we can also say (x2, y2) = (-2, 6)
So x%5B2%5D+=+-2, y%5B2%5D+=+6


Put this all together to get: x%5B1%5D+=+1, y%5B1%5D+=+-3, x%5B2%5D+=+-2, and y%5B2%5D+=+6

--------------------------------------------------------------------------------------------


Now use the distance formula to find the distance between the two points (1, -3) and (-2, 6)



d+=+sqrt%28%28x%5B1%5D-x%5B2%5D%29%5E2+%2B+%28y%5B1%5D+-+y%5B2%5D%29%5E2%29


d+=+sqrt%28%281+-+%28-2%29%29%5E2+%2B+%28-3+-+6%29%5E2%29 Plug in x%5B1%5D+=+1, y%5B1%5D+=+-3, x%5B2%5D+=+-2, and y%5B2%5D+=+6


d+=+sqrt%28%281+%2B+2%29%5E2+%2B+%28-3+-+6%29%5E2%29


d+=+sqrt%28%283%29%5E2+%2B+%28-9%29%5E2%29


d+=+sqrt%289+%2B+81%29


d+=+sqrt%2890%29


d+=+sqrt%289%2A10%29


d+=+sqrt%289%29%2Asqrt%2810%29


d+=+3%2Asqrt%2810%29


d+=+9.48683298050514

==========================================================

Answer:


The distance between the two points (1, -3) and (-2, 6) is exactly 3%2Asqrt%2810%29 units


The approximate distance between the two points is about 9.48683298050514 units



So again,


Exact Distance: 3%2Asqrt%2810%29 units


Approximate Distance: 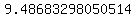9.48683298050514 units





The approximate distance is roughly 9.48683298050514 units

So you round that to the nearest hundredth to get 9.49 which is your final answer (if you decide to report the approximate answer over the exact answer)