The greatest common factor (GCF) of a polynomial is similar to the GCF of a real number. If I have 6 and 10, I could break them down into 2*3 and 2*5. The greatest factor is 5, but there is no 5 in the list for 6. So 2 is the greatest common factor since the number is in both 6 and 10.
The same idea is applied to polynomials. If we look at all of the coefficients to begin with (25,15,and 356) we would see that 5 could go into 25 and 15, but not into 356. Since the only factors of 25 are 1,5,and 25 (none of which go into 356) we cannot pull out a common factor from the coefficients. Now lets look at the variables. We can see a common theme of p's and q's, so those would part of our GCF. Looking at
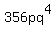There's only one p, and since there are at least one p in each polynomial, then p is part of our GCF.
Now lets look at q. The lowest degree of q is 
, so thats part of our GCF also.So our full GCF is
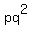
Notice that we can divide the GCF cleanly in all of these problems and get
,
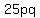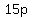, and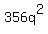 
This is like dividing real numbers by their factors
and 
Hope this helps.
(