SOLUTION: √5-√3-√2 over √5+√3+√2 please help me solve

Algebra ->  Radicals -> SOLUTION: √5-√3-√2 over √5+√3+√2 please help me solve       Log On


   

Question 712657: √5-√3-√2 over √5+√3+√2 please help me solve
Answer by jsmallt9(3758) About Me  (Show Source):
You can put this solution on YOUR website!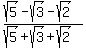
%28sqrt%285%29-sqrt%283%29-sqrt%282%29%29%2F%28sqrt%285%29%2Bsqrt%283%29%2Bsqrt%282%29%29
Rationalizing (which is what we are doing) a one-term denominator is simple. Rationalizing a two-term denominator is a little bit of a challenge. Rationalizing a three-term denominator, like in this problem, is a real challenge!

To understand how to do our problem, let's review how the two-term denominators are done. Rationalizing two-term denominators involves:
  • Changing the denominator so that there are no square roots.
  • Changing a denominator can be done by reducing the fraction or by multiplying the denominator and the numerator by the same expression. (Our fraction will not reduce so we will only be able to change the denominator by multiplication.)
  • Using multiplication to rationalize square roots involves finding a way to turn those square roots into square roots of a perfect square.
  • The pattern:
    %28a%2Bb%29%28a-b%29+=a%5E2-b%5E2
    shows us how to take a two-term expression, like a+b or a-b, multiply it by something and get a result of nothing but perfect squares.
Putting this all together, we can rationalize something like:
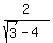
2%2F%28sqrt%283%29-4%29
Our denominator, with the "-" between the terms, will play the role of a-b. To rationalize this we multiply the numerator and denominator by a+b:
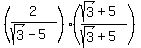
%282%2F%28sqrt%283%29-5%29%29%28%28sqrt%283%29%2B5%29%2F%28sqrt%283%29%2B5%29%29
Multiplying the denominator is easy because the pattern tells us how it will work out. On top we just use the Distributive Property:
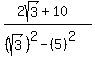
%282sqrt%283%29%2B10%29%2F%28%28sqrt%283%29%29%5E2-%285%29%5E2%29
Simplifying...
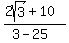
%282sqrt%283%29%2B10%29%2F%283-25%29
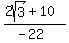
%282sqrt%283%29%2B10%29%2F%28-22%29
And the denominator is now rational.

Returning to the problem at hand...
Unfortunately there is no pattern that tells us how to turn a three-term denominator into an expression of nothing but perfect squares like there was above for two-term expressions. What we will be doing is using the same pattern,
%28a%2Bb%29%28a-b%29+=a%5E2-b%5E2, but in a clever way. To help us see this, I'm going to rewrite the fraction using grouping:

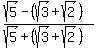
It help to see what we are doing if we think of 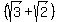sqrt%285%29 as our "a" and %28sqrt%283%29%2Bsqrt%282%29%29 as our "b". So our denominator is a+b. So we will multiply it and the numerator by a-b:

We can use our pattern to multiply the denominator again. And in the numerator we have, in effect, (a-b)(a-b). We have another pattern for this:
%28a-b%29%28a-b%29=a%5E2-2ab%2Bb%5E2. Using the two patterns we get:

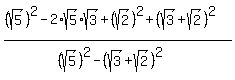
To square 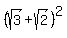%28sqrt%283%29%2Bsqrt%282%29%29%5E2 we have yet another pattern:
%28a%2Bb%29%28a%2Bb%29=a%5E2%2B2ab%2Bb%5E2. Using this pattern:

Simplifying...
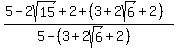
%285-2sqrt%2815%29%2B2%2B%283%2B2sqrt%286%29%2B2%29%29%2F%285-%283%2B2sqrt%286%29%2B2%29%29
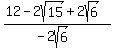
%2812-2sqrt%2815%29%2B2sqrt%286%29%29%2F%28-2sqrt%286%29%29
We still have a square root in the denominator so we are not finished. But we have gone from 3 square roots in the denominator to just 1 so we have made a lot of progress. And rationalizing a one-term denominator is easy. We can just multiply the numerator and denominator by sqrt%286%29:

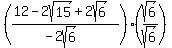
Simplifying...

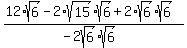
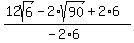
%2812sqrt%286%29-2%2Asqrt%2890%29%2B2%2A6%29%2F%28-2%2A6%29
%2812sqrt%286%29-2%2Asqrt%289%2A10%29%2B12%29%2F%28-12%29
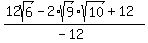
%2812sqrt%286%29-2%2Asqrt%289%29%2Asqrt%2810%29%2B12%29%2F%28-12%29
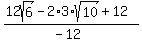
%2812sqrt%286%29-2%2A3%2Asqrt%2810%29%2B12%29%2F%28-12%29
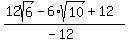
%2812sqrt%286%29-6%2Asqrt%2810%29%2B12%29%2F%28-12%29
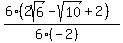
%286%282sqrt%286%29-sqrt%2810%29%2B2%29%29%2F%286%28-2%29%29
%28cross%286%29%282sqrt%286%29-sqrt%2810%29%2B2%29%29%2F%28cross%286%29%28-2%29%29
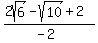
%282sqrt%286%29-sqrt%2810%29%2B2%29%2F%28-2%29
which is our simplified expression with a rational denominator. (If you prefer not to have a "-" in the denominator you can multiply the top and bottom by -1, giving: %28-2sqrt%286%29%2Bsqrt%2810%29-2%29%2F2)