Question 711000: Can you help me with simplifying radicals in algebra?
Answer by jsmallt9(3758)   (Show Source):
You can put this solution on YOUR website! Since you asked for general help and since radicals are used for all types of roots (square, cube, 4th, 5th, etc.) I can only provide very general help:- Determine which kind of root it is.
- (Note: "Radicand" is the name for whatever expression is found inside a radical.) Try to find as many factors of the radicand that are powers which match the type of root as possible. For square roots look for perfect square factors, for cube roots look for factors that are perfect cubes, etc. (Note: if the only perfect square/cube/etc. factor you can find is 1, then the radical will not simplify and you can stop here.)
- Rewrite the radicand in factored form. I like to put all the perfect square/cube/etc. factors in front and the other factor at the back.
- Use a property of radicals,
 , to break up the radical so that each perfect square/cube/etc. factor is in its own "personal" radical. The other factors, if any can all be lumped into a single radical. - The radical(s) containing the perfect square/cube/etc. factors will all simplify.
- If there were more than 1 perfect square/cube/etc. factors then simplify/multiply what is outside the radical.
Let's look at a couple of examples:
 (assuming x and y are both positive)
Finding perfect square factors:
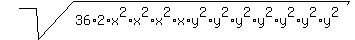
Reordering to put the perfect squares in front:
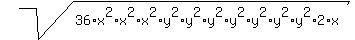
Separating the perfect squares into their own radical(s):
Each square root of a perfect square simplifies:
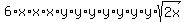
Simplify what's outside:
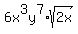
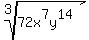
Finding perfect cube factors. (Note:  and 8 is a factor of 72.)
Reordering to put the perfect cubes in front:
Separating the perfect cubes into their own radical(s):
Each cube root of a perfect cube simplifies:
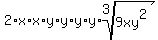
Simplify what's outside:
|
|
|
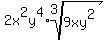
