Only one kind of root is called a "SQUARE" root. Sometimes students
get the wrong impression that all roots are called "SQUARE" roots, but
this is false.
simplify by factoring 5 square root 96x^12y^15
Did you mean this 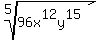 ?
If so that is NOT a "SQUARE" root but a FIFTH root.
If it were as you stated it would be
?
If so that is NOT a "SQUARE" root but a FIFTH root.
If it were as you stated it would be 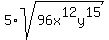 which is an entirely different problem.
If you meant the FIFTH root, not the SQUARE root, then you change
which is an entirely different problem.
If you meant the FIFTH root, not the SQUARE root, then you change
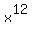 to
to 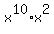 because 10 is the largest exponent
divisible by 5. We also change
because 10 is the largest exponent
divisible by 5. We also change 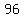 to
to 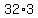 or
or 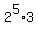 .
We do not need to change
.
We do not need to change 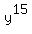 because 15 is already divisible
by 5, the index of the 5th root.
because 15 is already divisible
by 5, the index of the 5th root.
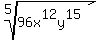 =
= 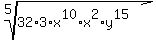 =
=
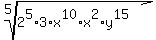 =
Now we divide each exponent that is divisible by 5 and bring it out
from under the radical with the exponent divided by the index 5:
=
Now we divide each exponent that is divisible by 5 and bring it out
from under the radical with the exponent divided by the index 5:
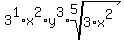 and you can drop the 1 exponent for x
and you can drop the 1 exponent for x
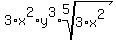 If you really meant "SQUARE ROOT", like this:
If you really meant "SQUARE ROOT", like this:
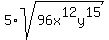 Then the index is understood to be 2. I'll put the index:
Then the index is understood to be 2. I'll put the index:
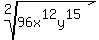 then you do not need to change
then you do not need to change 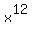 because 12 is already
divisible by 2. We change
because 12 is already
divisible by 2. We change 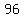 to
to 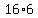 or
or 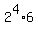 , so
that the exponent 4 is divisible by 2.
We change
, so
that the exponent 4 is divisible by 2.
We change 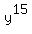 to
to 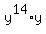 .
.
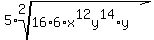
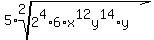 Now we divide each exponent by 2 that is divisible by 2 and bring it out
from under the radical with the exponent divided by the index 2:
Now we divide each exponent by 2 that is divisible by 2 and bring it out
from under the radical with the exponent divided by the index 2:
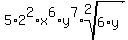 =
=
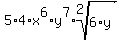 and we drop the 2 index because it's understood when the root is a
SQUARE root and not some other root such as the FIFTH root.
and we drop the 2 index because it's understood when the root is a
SQUARE root and not some other root such as the FIFTH root.
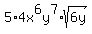 =
=
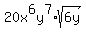 Edwin
Edwin