Question 647491: Hello, My problem is - If x = -2, y = 3, and z = 4, which expression has the greatest value?
a. z(x-y)
b. z(x-y) to the 2nd power - x
c. z(x-y) to the 3rd power + x
d. z over x - xy
-I have looked several chapters back and still can't find a thing on how to do this.
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website! a)
z(x-y)
4(-2-3) ... Plug in x = -2, y = 3, and z = 4
4(-5)
-20
So z(x-y) = -20 when x = -2, y = 3, and z = 4
-------------------------------------------------------------------------------
b)
z(x-y)^2 - x
4(-2-3)^2 - (-2) ... Plug in x = -2, y = 3, and z = 4
4(-2-3)^2 + 2
4(-5)^2 + 2
4(25) + 2
100 + 2
102
So z(x-y)^2 - x = 102 when x = -2, y = 3, and z = 4
So far, choice B is the largest.
-------------------------------------------------------------------------------
c)
z(x-y)^3 + x
4(-2-3)^3 + (-2)
4(-2-3)^3 - 2
4(-5)^3 - 2
4(-125) - 2
-500 - 2
-502
So z(x-y)^3 + x = -502 when x = -2, y = 3, and z = 4
Choice C is NOT larger than choice B. So choice B is still the largest.
-------------------------------------------------------------------------------
d)
I'm assuming this one is 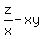
z/x - xy
4/(-2) - (-2)(3)
-2 - (-2)(3)
-2 - (-6)
-2 + 6
4
So z/x - xy = 4 when x = -2, y = 3, and z = 4
================================================================================================
Answer:
Choice B is has the greatest value.
--------------------------------------------------------------------------------------------------------------
If you need more help, email me at jim_thompson5910@hotmail.com
Also, please consider visiting my website: http://www.freewebs.com/jimthompson5910/home.html and making a donation. Thank you
Jim
--------------------------------------------------------------------------------------------------------------
|
|
|