Question 623092: simplify
root symbol 39a^3b^5/root symbol 13a2b
I am having difficulty with this can you help please????
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! I assume by "root symbol" you mean square root. (In the future, please specify which kind of root.) I also assume that "13a2b" means 
There are several ways to deal with a fraction of square roots. My prefernce is to do the following:- Use the
 property to join the two square roots into one. property to join the two square roots into one. - Reduce the fraction. (Note: If you're clever you will keep in mind step 3 and maybe not reduce the fraction as fully as possible. For example, if you had
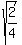 then you would not reduce the fraction because step 3 wants perfect square denominators. 4 is already a perfect square. If we reduce 2/4 to 1/2 then we would no longer have a perfect square denominator. And we would end up changing 1/2 back to 2/4 in step 3.) then you would not reduce the fraction because step 3 wants perfect square denominators. 4 is already a perfect square. If we reduce 2/4 to 1/2 then we would no longer have a perfect square denominator. And we would end up changing 1/2 back to 2/4 in step 3.) - If there still is a denominator, then make sure it is a perfect square.
- If there still is a denominator, then use the
 property again, this time in the other direction -- to split the numerator from the denominator. property again, this time in the other direction -- to split the numerator from the denominator. - Simplify any remaining square roots and fractions.
Let's see this in action:
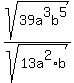
1. Join the square roots:
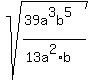
2. Reduce the fraction (maybe not fully).
The entire denominator cancels out leaving:

or just

3. If there's a still denominator, ...
There is no denominator.
4. If there's a still denominator, ...
There is no denominator.
5. Simplify any remaining square roots and fractions.
To simplify a square root, look for perfect square factors of the radicand (the expression inside). There are not prefect square factors in the 3 or the a. But there are perfect square factors in  . When I factor out the perfect squares I like to put those factors in front: . When I factor out the perfect squares I like to put those factors in front:
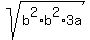
Then you use another property of radicals,  , split the square root so that eah perfect square factor is in its own square root: , split the square root so that eah perfect square factor is in its own square root:
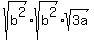
The square roots of the perfect squares simplify:
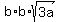
which simplifies to:
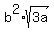
|
|
|