Question 571813: Find the distance between the two points and the midpoint. (2,1) and (-4,-2). Please help!! I am stuck! I guess I don't understand how to figure out the part with the radicals. I got radical 41 but haave no idea what to do after that.
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website!  Points A and B are your points. Points A and B are your points.
The distance is that red hypotenuse of the red and blue right triangle, so its length is

So the length of the segment is
 = =
Of course, when you do not have the picture, it gets harder to get the numbers straight into the formula. To keep them straight, I write the coordinates of the points right above my calculation, and in the order I'm going to take them. Then I start filling numbers into

I may write (-4,-2) and (2,1) and on the next line use the coordinates in the same order:

If I wrote (2,1) and (-4,-2), the next line would be

I made the midpoint part of a little red, blue and green right triangle. You know it's similar to the large red and blue right triangle. Because the midpoint is halfway between A and B, the distance from the midpoint to A is half of the distance between A and B. So the hypotenuse of the little right triangle is half of the hypotenuse of the large right triangle. And because both triangles are similar, each leg of the little triangle is half of the corresponding leg of the large triangle. That means that the x and y coordinates of the midpoint will be right in the middle between the x and y coordinates of A and B and we can calculate them as the averages of those coordinates.
Keeping numbers straight again, the endpoints are (-4,-2) and (2,1)
midpoint = (  , , 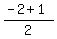 )=(-2/2,-1/2)=(-1,-1/2) )=(-2/2,-1/2)=(-1,-1/2)
|
|
|