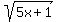 +
+ 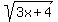 =
=  To make things easier, let the radicals be letters and only
replace them when they get squared:
let A =
To make things easier, let the radicals be letters and only
replace them when they get squared:
let A = 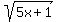 , B =
, B = 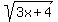 , C =
, C = 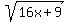 then A² = 5x+1, B² = 3x+4, C² = 16x+9
Since A and B are on the same side they will be multiplied, so
(AB)² = (5x+1)(3x+4) = 15x² + 23x + 4
The original problem becomes
A + B = C
Square both sides:
(A + B)² = C²
A² + 2AB + B² = 16x + 9
5x + 1 + 2AB + 3x + 4 = 16x + 9
8x + 5 + 2AB = 16x + 9
2AB = 8x + 4
AB = 4x + 2
(AB)² = (4x + 2)²
15x² + 23x + 4 = 16x² + 16x + 4
0 = x² - 7x
0 = x(x - 7)
x = 0; x - 7 = 0
x = 7
We must check both 0 and 7 for irrational solutions:
Checking x = 0
then A² = 5x+1, B² = 3x+4, C² = 16x+9
Since A and B are on the same side they will be multiplied, so
(AB)² = (5x+1)(3x+4) = 15x² + 23x + 4
The original problem becomes
A + B = C
Square both sides:
(A + B)² = C²
A² + 2AB + B² = 16x + 9
5x + 1 + 2AB + 3x + 4 = 16x + 9
8x + 5 + 2AB = 16x + 9
2AB = 8x + 4
AB = 4x + 2
(AB)² = (4x + 2)²
15x² + 23x + 4 = 16x² + 16x + 4
0 = x² - 7x
0 = x(x - 7)
x = 0; x - 7 = 0
x = 7
We must check both 0 and 7 for irrational solutions:
Checking x = 0
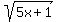 +
+ 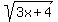 =
= 
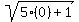 +
+ 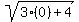 =
= 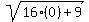
 +
+ 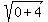 =
= 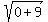
 +
+  =
= 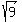 1 + 2 = 3
3 = 3
So x = 0 is a solution
Checking x = 7
1 + 2 = 3
3 = 3
So x = 0 is a solution
Checking x = 7
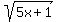 +
+ 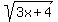 =
= 
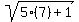 +
+ 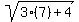 =
= 
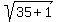 +
+ 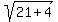 =
= 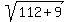
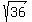 +
+  =
=  6 + 5 = 11
11 = 11
So x = 7 is also a solution
So x = 0 and x = 7 are the solutions.
Edwin
6 + 5 = 11
11 = 11
So x = 7 is also a solution
So x = 0 and x = 7 are the solutions.
Edwin