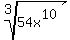 The root is cube root which is the 3rd root, so we want to get
as many exponens under it as possible that can be divided evenly by 3.
We break up 54 as 27·2, then as 9·3·2 and then as 3·3·3·2 and then as 3³·2
So instead of 54 we write 3³·2
The root is cube root which is the 3rd root, so we want to get
as many exponens under it as possible that can be divided evenly by 3.
We break up 54 as 27·2, then as 9·3·2 and then as 3·3·3·2 and then as 3³·2
So instead of 54 we write 3³·2
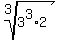 That has one exponent that is divisible by 3.
Now lets break x10 up as x9·x1, because
9 is divisible by 3. So we write this:
That has one exponent that is divisible by 3.
Now lets break x10 up as x9·x1, because
9 is divisible by 3. So we write this:
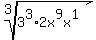 Now we can divide the two exponents 3 and 9 by 3 getting 1 and 3,
and take them out of the radical and put the resulting exponentials
out in front of the radical:
Now we can divide the two exponents 3 and 9 by 3 getting 1 and 3,
and take them out of the radical and put the resulting exponentials
out in front of the radical:
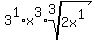 Erase the 1 exponents:
Erase the 1 exponents:
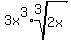 Edwin
Edwin