Question 515532: For what value of 2x^2-3x+c=0 have one and only one real root?
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website! So, for what value of c will  have one and only one real root? To answer this question, let's think about the quadratic formula: have one and only one real root? To answer this question, let's think about the quadratic formula:

Specifically take note of the 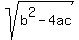 . What's inside of this radical is known as the determinant, because it determines how many roots there will be. . What's inside of this radical is known as the determinant, because it determines how many roots there will be.
 this this 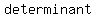 is is 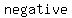 , then there are , then there are   solutions. This is because you can't take the square root of a negative number without using imaginary numbers. Therefore, a negative determinant implies no real roots. solutions. This is because you can't take the square root of a negative number without using imaginary numbers. Therefore, a negative determinant implies no real roots.
 this this 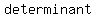 is is 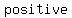 , then there are , then there are   solutions. This is because of the ± in the quadratic formula. solutions. This is because of the ± in the quadratic formula.
 the the 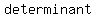 happened to be happened to be  , then you'd have , then you'd have  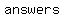 : one you would have to add the : one you would have to add the  , and the other you would have to subtract the , and the other you would have to subtract the  . .
 the the 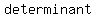 is is  , then there is , then there is  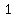  solution. This is because + or - zero leaves the quadratic formula unchanged. In summary: solution. This is because + or - zero leaves the quadratic formula unchanged. In summary:
One real solution: 
Two real solutions: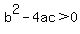
No real solutions: 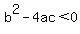
So let's solve to see when the determinant equals zero, so there will be only one real root. We will use the a, b, and c values from the equation you provided earlier.




Let's set the determinant equal to zero, and then substitute the known values:






 must be equal to must be equal to  for the equation to have one and only one real root. for the equation to have one and only one real root.
|
|
|