Question 482538: please i need help with this problem:
thank you so much for your time!!
Answer by bucky(2189)   (Show Source):
You can put this solution on YOUR website! Given:
.
To solve, square both sides. For the left side this means multiplying:
.
.
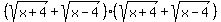
Use the FOIL system. In the two sets of parentheses, multiply FIRST terms, then multiply OUTSIDE terms, then multiply INSIDE terms, and finally multiply LAST terms.
.
Firsts: 
.
Outsides: 
.
Insides: 
.
Finally, Lasts: 
.
Add all these results together and you have:
.
.
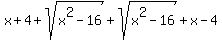
The two terms containing the radicals are identical. Therefore, they can be added and the overall expression becomes:
.
.
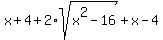
Note that the +4 and the -4 cancel each other out and also the x + x sum to 2x. Therefore, the left side that we squared simplifies to:
.
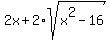 <--- this is the left side squared
.
Now let's return to the original equation and square the right side as follows:
.
 <--- this is the right side squared
.
And the square of the left side must equal the square of the right side as follows:
.
.
Note that a term 2x appears on both sides. Therefore, subtract 2x from both sides and the equation reduces to:
.
.
Divide both sides by 2 and you get:
.
.
Now get rid of the radical by squaring both sides again and you have
.
.
Get rid of the -16 on the left side by adding 16 to both sides and you have:
.
.
And finally, solve for x by taking the square root of both sides. The result is:
.
.
And that's the answer. You can return to the original equation that you were given to solve and substitute 5 for x to get:
.
.
Letting x = 5 results in this becoming:
.
.
and this simplifies to:
.
.
and finally our check shows that by taking the square roots of the three numbers:
.
.
which means that if x = 5 the original equation balances. Both sides are equal.
.
Hope this helps you to understand the problem and how to work it.
|
|
|
