Question 468681: Divide Then simplify by taking roots, if possible Assume that all expressions under radical represent positive numbers
V63xy^3 / V9x
the v's are square root symbols and ^means it is raising to that power this is also a fraction, so it is the square root of 63xy^3 (numerator) over the square root of 9x (denominator)
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! In algebra.com, square root of a number is officially shown as sqrt(x).
any root of a number greater than that would be shown as root(n,x) where n is the power of the root and x is the number.
for example:
square root of 2 would be shown as sqrt(2)
cube root of 2 would be shown as root(3,2)
5th root of 2 would be shown as root 5,2)
etc.
If you are going to continue to use the V symbol, then enclose the expression that is within the root sign in parentheses.
Your problem could be restated as:
V(63xy^3) / V(9x)
Algebra.com notation would show it as:
sqrt(63xy^3) / sqrt(9x)
If you put 3 curly brackets in front and 3 curly brackets in back, then the algebra.com formula generator would show it as:
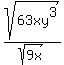
The front curly brackets look like {.
The back curly brackets look like }.
On your keyboard, they would be to the right of the P.
They would be Shift [ and Shift ] (upper case letters on those keys).
That's on my keyboard which is a Toshiba. Your keyboard might be different but possibly not.
Anyway, back to your problem.
you have sqrt(63xy^3) / sqrt(9x).
This is equivalent to sqrt(63xy^3/9x).
The x in the numerator and the x in the denominator cancel out and you are left with sqrt(63y^3/9)
9 goes into 63 seven times and you are left with sqrt(7y^3)
y^3 is equivalent to y^2 * y which means you can take the sqrt of y^2 and make it a y outside the square root sign to get y*sqrt(7y).
That should be your final answer.
sqrt(63xy^3) / sqrt(9x) is equivalent to y*sqrt(7y).
In algebra.com formula generator format, that would look like:
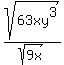 is equivalent to is equivalent to 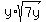 . .
I have confirmed that the original equation gives you the same answer as the final equation by substituting a value for x and a value for y and solving both the original equation and the final equation.
Since the answer in both cases came out the same, I am reasonably confident I did it right.
|
|
|