
Multiply under the radicals and get
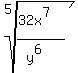 Break it into the quotient of two fifth roots:
Break it into the quotient of two fifth roots:
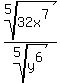 The power of y in the denominator must be a
multiple of 5, so it needs to be multiplied by
y4 so that it will become y10.
So we multiply the entire fraction by
The power of y in the denominator must be a
multiple of 5, so it needs to be multiplied by
y4 so that it will become y10.
So we multiply the entire fraction by 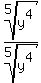
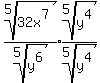 We multiply under the radicals:
We multiply under the radicals:
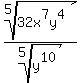 The denominator is simplified by dividing the exponent 10
by the index of the root 5, getting exponent 2, and
eliminating the radical, so we have
The denominator is simplified by dividing the exponent 10
by the index of the root 5, getting exponent 2, and
eliminating the radical, so we have
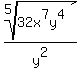 Now we will simplify the numerator.
Write 32 as 25
Write x7 as x5x2
Now we will simplify the numerator.
Write 32 as 25
Write x7 as x5x2
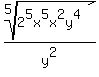 Finally you can take the two fifth powers out
of the fifth root and have 2x in front of the
radical:
Finally you can take the two fifth powers out
of the fifth root and have 2x in front of the
radical:
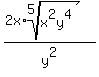 Edwin
Edwin