Question 424626: A 62 foot guy-wire makes an angle of 60 degrees with the ground and is attached to a telephone pole. Find the distance from the base of the pole to the point on the pole where the wire is attached. Express your answer to the nearest tenth of a foot.
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! With the pole presumed to be perpendicular to the ground and with a 60 degree angle, the triangle formed by the ground, the pole and the wire is a 30/60/90 right triangle. It might help you understand the following if you draw a diagram of this triangle.
From Geometry (and maybe in Trigonometry, too) you learned that there is a certain relationship between the sides of all 30/60/90 right triangles (no matter what size they are):- The hypotenuse is always twice as large as the side opposite the 30 degree angle. (Or to put it another way, the side opposite the 30 degree angle is 1/2 as large as the hypotenuse.)
- The side opposite the 60 degree angle is always
 times the side opposite the 30 degree angle. times the side opposite the 30 degree angle.
In this problem we are given the length of the wire, which is the hypotenuse of the triangle. So the hypotenuse is 62 feet. The side opposite the 30 degree angle will therefore be half of this: 31 feet. And the side opposite the 60 degree angle, the pole, will be 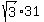 or or 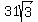 feet. feet.
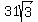 is an exact expression for the distance from the ground to where the wire is attached to the pole. To find the requested decimal answer, get out your calculator, find the square root of 3, multiply it by 31 and round the answer to the nearest tenth. is an exact expression for the distance from the ground to where the wire is attached to the pole. To find the requested decimal answer, get out your calculator, find the square root of 3, multiply it by 31 and round the answer to the nearest tenth.
|
|
|