Question 424399: 2 square root of 2 plus + square root of 32
Answer by jsmallt9(3758)   (Show Source):
You can put this solution on YOUR website!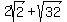 
Like radical terms are the same types of root with the same radicands. (The expression inside a radical is called a radicand.) Your terms are both the same kind of root, square root, but their radicands, 2 and 32, are not the same. So we cannot add these terms together.
Although we cannot add these square roots we can simplify them if their radicands have any perfect square factors (other than 1). The first radicand, 2, is a prime number so it has no perfect square factors. But the second radicand, 32, does have a perfect square factor so we can simplify that square root.
First we rewrite the radicand in factored form:
Then we use a property of radicals,  , to split the square root:
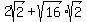
The square root of the perfect square simplifies:
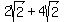
We have now simplified both square roots. And if you look again, you will see that we now have like terms! So now we can add them. And exactly like 2x + 4x = 6x:
So you expression simplifies down to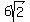 
|
|
|
