Question 419751: 6 radical 128 + 3 radical 8
Answer by jsmallt9(3758)   (Show Source):
You can put this solution on YOUR website! I assume by "radical" you mean "square root". They are not the same thing. The radical symbol is the name for that symbol that looks a little like the symbol we use when doing long division. Radical symbols are used for all kinds of roots: square roots, cube roots, 4th roots, etc. For example each of the following has a radical symbol:
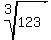
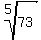
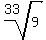
but only the first one is a square root. Please use proper terminology so that your problems are clear. Tutors are more likely to respond if the problem is clearly stated.
I also have to guess that the problem is to simplify the expression. Please provide the instructions for the problem along with the expressions, equations or inequalities.
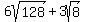
These are not like terms so we cannot add them. (Like terms with radicals are the same kind of root (square, cube 4th, etc.) with the same radicands. (The expression inside a radical is called the radicand.) These two term are both square roots but their radicands, 128 and 8, are different.
Although we cannot add these terms, we can simplify the individual square roots. Simplifying a square root primarily involves finding perfect square factors, if any, of the radicand. Looking at 128 and 8 we should be able to figure out that they both have perfect square factors. So both of these square roots will simplify.
To simplify the square roots we start by factoring the radicands using perfect square factors. (Note: not all the factors have to be perfect squares.):
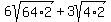
Next we use a property of radicals,  , to put each factor into its own square root:
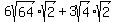
The square roots of the perfect squares will simplify:
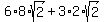
which simplifies to:
We have now simplified the square roots. Not only that, but the two terms are now like terms (both are square roots with a radicand of 2). So we can now add them together. Adding radical terms is a lot like adding terms with variables. In fact it can help to look at the square roots as variables. Exactly like 48x + 6x = 54x ...
So you final simplified expression is
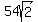
Note: After we simplified the square roots we ended up with like terms. This does not always happen. So you will not always be able to add (or subtract) the terms, even after simplifying the square roots.
|
|
|
