SOLUTION: square root (x+3) ^8 would it be absolute value x+3?

Algebra ->  Radicals -> SOLUTION: square root (x+3) ^8 would it be absolute value x+3?      Log On


   

Question 405407: square root (x+3) ^8
would it be absolute value x+3?
Answer by jsmallt9(3758) About Me  (Show Source):
You can put this solution on YOUR website!
Please use parentheses to make things clear. I cannot tell if the exponent of 8 applies to the (x+3) or to the sqrt(x+3). So it could be
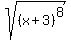
sqrt%28%28x%2B3%29%5E8%29
or
%28sqrt%28x%2B3%29%29%5E8
These expressions are different. Tutors are more likely to help when the problem is clear. (This might be why you have gotten no responses in two days.)

In this particular case, both expression simplify to the same thing so I will go ahead and solve the problem. One way to simplify this is to use a fractional exponent for the square root:
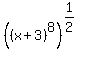
%28%28x%2B3%29%5E8%29%5E%281%2F2%29
or
%28%28x%2B3%29%5E%281%2F2%29%29%5E8
When raising a power to a power the rule is to multiply the exponents. And since both 8 * 1/2 and 1/2 * 8 are both 4, both of the expressions above work out to be:
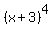
%28x%2B3%29%5E4
And since something to the 4th power cannot be negative, absolute value is not needed.

Simplifying with the radical form is a little more difficult. I'll do each of the possible expressions separately.
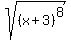
sqrt%28%28x%2B3%29%5E8%29
To simplify this square root we factor the radicand (the expression inside) into perfect squares:
sqrt%28%28x%2B3%29%5E2%2A%28x%2B3%29%5E2%2A%28x%2B3%29%5E2%2A%28x%2B3%29%5E2%29
Then we use a property of radicals, root%28a%2C+p%2Aq%29+=+root%28a%2C+p%29%2Aroot%28a%2C+q%29, to split the square root of a product into a product of the square roots fo the factors:

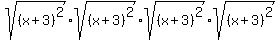
Each of the square roots simplify. In this case, since we do not know if x+3 is positive, negative or zero, we use absolute values:
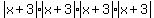
abs%28x%2B3%29%2Aabs%28x%2B3%29%2Aabs%28x%2B3%29%2Aabs%28x%2B3%29
or
%28abs%28x%2B3%29%29%5E4
Again, since anything to the 4th power will never be negative, we can remove the absolute value:
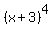
%28x%2B3%29%5E4

For
%28sqrt%28x%2B3%29%29%5E8
Let's start by writing it out without the exponent of 8:

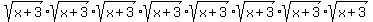
Since multiplication is Associative we can group these as we choose:

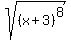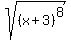Each grouped pair of factors simplifies. (Note: since the original radicand of this expression was x+3 we know that x+3 cannot be negative. Therefore, aboslute values will not be needed on this expression. In the other possible expression, sqrt%28%28x%2B3%29%5E8%29, the radicand is %28x%2B3%29%5E8. With %28x%2B3%29%5E8, the x+3 can be anything, including negative, because after raise it to the 8th power it never be negative. Since the x+3 in sqrt%28%28x%2B3%29%5E8%29 could be negative, we needed the absolute value, at least temporarily.) So now we have:
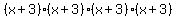
%28x%2B3%29%28x%2B3%29%28x%2B3%29%28x%2B3%29
or
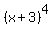
%28x%2B3%29%5E4

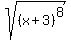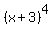So both sqrt%28%28x%2B3%29%5E8%29 and %28sqrt%28x%2B3%29%29%5E8 simplify to %28x%2B3%29%5E4 no matter which way you simplify it.