Question 398823: Please help, I am soooo lost with 2 problems:
1: Cube Root of 270x divided by cube root of 10xy^2
2: Cube root of x^2 divided by cube root of 4
Thank you so much!
Found 2 solutions by josmiceli, jsmallt9:
Answer by josmiceli(19441)   (Show Source):
Answer by jsmallt9(3758)  (Show Source):
You can put this solution on YOUR website! With expressions like these, a radical over the same kind of radical, I like to use the following procedure:- Use the property
 to combine the two radicals into a single radical. - Reduce the fraction inside the radical, if possible.
- If the denominator is not a perfect power of the type of radical, then multiply the numerator and denominator by some expression so that the denominator becomes a perfect power of the type of radical.
- Use the same property as step 1, only in reverse, to split the radical back to a radical over a radical.
- Simplify. If the previous steps were done correctly, there should be no radicals remaining in the denominator.
Let's see this in action.
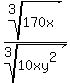
1) Combine radicals:
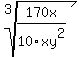
2) Reduce the fraction inside. The x's cancel and a factor of 10 cancels leaving:
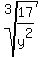
3) If the denominator is is not a perfect power of the type of radcial, then multiply the numerator and denominator by whatever makes the denominator a perfect power of the type of radical. Since we are working with cube roots, we are looking to make the denominator a perfect cube. All we need is another factor of y:
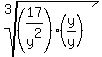
which simplifies to:
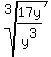
4) Split the radical:
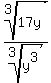
5. Simplify.
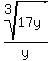
Since there are no perfect cube factors in 17y, the radical in the numerator will not simplify further.
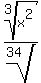
1. Combine the radicals:
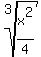
2. Reduce the fraction. This fraction will not reduce.
3. Make the denominator a power of the type of radical. The "nearest" perfect cube to 4 is 8. So we just have to multiply the numerator and denominator by 2:
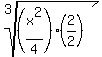
which simplifies to:
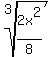
4. Split the radical:
5. Simplify.
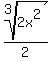
There are no perfect cube factors in  so the numerator will no simplify any further.
Note 1: The procedure I've described is not the only way to simplify your expressions. But it is pretty efficient at handing radical over radical expression.
Note 2: Any procedure used correctly should simplify your expressions to the same results as we got above.
Note 3: If the radicals are of different types then use fractional exponents to make them the same type. For example:
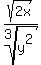
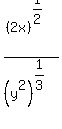
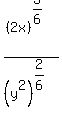
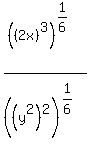
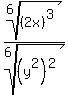
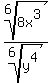
Now that the radicals are both 6th roots, we can use the procedure above:
1. Combine:
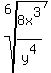
2. Reduce. This will not reduce.
3. Make the denominator a power of the type of radical:
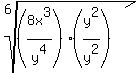
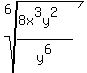
4. Split
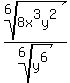
5. Simplify. Since sixth roots are supposed to be positive and since we do not know if y is positive, we should use absolute value when simplifying  :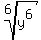
|
|
|
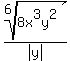
