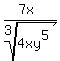Break the denominator down into prime factors:
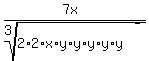We now must decide what factors the denominator would need in order
for it to become a perfect cube. We need three or a multiple of
three of each factor:
We have 2*2, which is two factors, so we need one more factor of 2
so we'll have three factors of 2.
We have x, which is one factor, so we need two more factors of x
so we'll have three factors of x.
We have y*y*y*y*y, which is five factors, so we need one more factor of y
so we'll have a multiple of three, that is, six factors of y.
So we create another cube root which has what we need in it, one
factor of 2, two factors of x and one factor of y. That is, we
create this cube root:
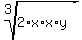Then we place it over itself so that the value will be 1.
And we can now multiply it by the original expression without
changing its value since we are actually only multiplying by 1.
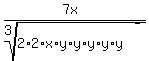
Now we multiply under the radicals on the bottom:
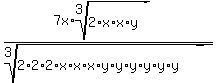Now we group the like factors in the bottom into groups of three:
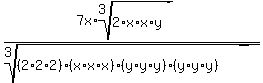Now we write each group of three as the cube of a single factor:
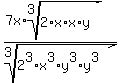Now take individual cube roots:
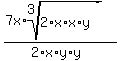Write the 
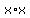in the top as 
and the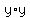 
in
the bottom as 
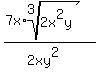You can perhaps figure out a shorter way than this, but this method
will always work. Do them this way and I think you will figure out
a shortcut after doing a few this longer but easier to follow way.
Edwin
