Question 383712: PLEASE HELP ME!!! rationalize the denominator. assume all expressions under radical represent positive numbers. √(16/9xy^2) problem is all under the radical.
Answer by jsmallt9(3758)   (Show Source):
You can put this solution on YOUR website! 
As often happens in Math, there are sever ways to do this. The way I like to do it is:
1. Make the denominator a perfect square.
9 is a perfect square and so is  . Only the x in the denominator is not a perfect square. To make the denominator a perfect square, then, we just have to change x into  somehow. This can be done by simply multiplying the numerator and denominator of the fraction by x:
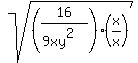
which gives us:
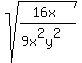
Now we can use a property of radicals,  , to separate the numerator and denominator into separate square roots:
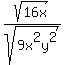
The denominator, being the square root of a perfect square, simplifies easily:
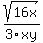
The numerator has a perfect square factor, 16. So we can simplify that, too.
Using another property of radicals,  , we can separate the factors into their own square roots:
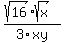
And the square root of 16 is 4:
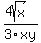
This is a simplified expression with a rational denominator.
|
|
|
