Question 360154: how to solve this radical equation(x^2+7)^-3/2=1/64
Answer by jsmallt9(3758)   (Show Source):
You can put this solution on YOUR website! 
Solving for x means we want x by itself on one side of the equation. So somehow, using proper Math, we need to "peel away" both exponents and the +7 on the left side. I use the phrase "peel away" because we usually remove the outer later and repeat as we work out way in to where the "x" is.
So we want to start by eliminating the exponent of -3/2. Of course, exponents never actually go away. They just become "invisible". And the only exponent that we don't have to write is 1. So what we really want is to change the exponent of -3/2 into a 1 somehow. And when do exponents change? Answer: when multiplying (we add the exponents), dividing (we subtract the exponents) or raising to a power (we multiply the exponents). The way we will turn the exponent of -3/2 into a 1 will be by raising both sides of the equation to a certain power. And what will that power be? Answer: The number we can multiply -3/2 by to get a 1. If you know about reciprocals, then you know that when you multiply them you always get 1. So we will raise each side of the equation by the reciprocal of -3/2 power. The reciprocal of -3/2 is -2/3:
On the left side we already know that the exponent turns into a 1 and "disappears". On the right side we want to raise 1/64 to the -2/3 power. If you are comfortable with exponents then this is fairly simple. If you are not comfortable with exponents, then I find that it can help to look at the exponent in factored form:
Looking at the factors of the exponent:- The -1 means we will be doing a reciprocal
- The 2 means we will be squaring
- The 1/3 means we will be doing a cube root.
And since multiplication is Commutative, we can do these three things in any order we choose! And I am going to choose an order that makes things as easy as possible. Since 1/64 is a fraction and its reciprocal is 64 (a nice whole number), I am going to start with the reciprocal:
Next, since calculating 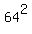 is not simple and since  (and therefore the cube root of 64 is 4 (another nice whole number)), I will do the cube root:
And squaring 4 is very simple giving us:
Now we have a quadratic equation to solve. So we want one side to be zero. Subtracting 16 from each side we get:
Now we can factor (or use the Quadratic Formula). As a difference of squares this factors very easily:
From the Zero Product Property we know that this (or any) product can be zero only if one of the factors is zero. So:
x + 3 = 0 or x - 3 = 0
Solving these we get:
x = -3 or x = 3
So there are two solutions to your equation.
|
|
|
