Because when written with a radical Ö a square
root or a 4th root 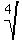 , or a 6th root
, or a 6th root 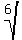 , 8th root
, 8th root
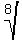 , or any root with an EVEN index can never represent a negative
number (that's not true with odd index roots).
Therefore your equation
, or any root with an EVEN index can never represent a negative
number (that's not true with odd index roots).
Therefore your equation
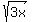

 has a square root written with a radical on the left, which means that
the left side is NOT negative. Yet it is equal to a negative number on
the right, which means it can have no real solution.
Edwin
has a square root written with a radical on the left, which means that
the left side is NOT negative. Yet it is equal to a negative number on
the right, which means it can have no real solution.
Edwin