
Put parentheses around the numeratior and denominator:
 Form the conjugate of the denominator by changing the
sign of the second term, that is,
Form the conjugate of the denominator by changing the
sign of the second term, that is, 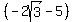 , put it over
itself,
, put it over
itself, 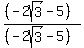 , which has value 1.
So we may multiply it by the original without changing the value
, which has value 1.
So we may multiply it by the original without changing the value


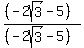



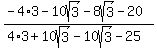

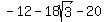

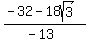 That's what you got but you can simplify it by multiplying by
That's what you got but you can simplify it by multiplying by 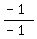
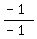

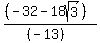

 Edwin
Edwin