That's a clever way you came up with to make a cube
root radical. But you can put this
root(3,-432x^17y^12)
between triple brackets (three of these "{" in a row on the
left and three of these "}" in a row on the right and you get
this posted:
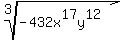 Any odd root of a negative number is negative so
we first of all take the negative sign out. (You
can only do this with odd roots, not even roots).
So first we take out the negative sign:
Any odd root of a negative number is negative so
we first of all take the negative sign out. (You
can only do this with odd roots, not even roots).
So first we take out the negative sign:
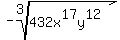 Next we break 432 into prime factors:
Next we break 432 into prime factors:

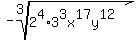 Divide the index 3 into each exponent:
Divide index 3 into 4, the exponent of 2
1
3)4
3
1
The quotient is 1 and the remainder is 1
The quotient tells us what power of 2 comes out of the
radical and the remainder tells us what power of 2 remains
under the radical. So
Divide the index 3 into each exponent:
Divide index 3 into 4, the exponent of 2
1
3)4
3
1
The quotient is 1 and the remainder is 1
The quotient tells us what power of 2 comes out of the
radical and the remainder tells us what power of 2 remains
under the radical. So 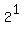 comes out in front of the
radical and
comes out in front of the
radical and 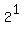 remains under the radical:
remains under the radical:
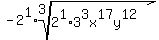 and of course we can erase the 1 exponents:
and of course we can erase the 1 exponents:
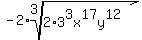 Divide index 3 into 3, the exponent of 3
1
3)3
3
0
The quotient is 1 and the remainder is 0
The quotient tells us what power of 3 comes out of the
radical and the remainder tells us what power of x remains
under the radical. So
Divide index 3 into 3, the exponent of 3
1
3)3
3
0
The quotient is 1 and the remainder is 0
The quotient tells us what power of 3 comes out of the
radical and the remainder tells us what power of x remains
under the radical. So  comes out in front of the
radical and no power of 3 remains under the radical, or
you can say
comes out in front of the
radical and no power of 3 remains under the radical, or
you can say  which is just 1 remains under the
radical, but we don't even have to write it:
which is just 1 remains under the
radical, but we don't even have to write it:
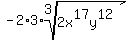 Now we can multiply the -2 and the 3 in front of the radical
and get:
Now we can multiply the -2 and the 3 in front of the radical
and get:
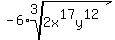 Divide index 3 into 17, the exponent of x
5
3)17
15
2
The quotient is 5 and the remainder is 2
The quotient tells us what power of x comes out of the
radical and the remainder tells us what power of x remains
under the radical. So
Divide index 3 into 17, the exponent of x
5
3)17
15
2
The quotient is 5 and the remainder is 2
The quotient tells us what power of x comes out of the
radical and the remainder tells us what power of x remains
under the radical. So 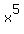 comes out in front of the
radical and
comes out in front of the
radical and  remains under the radical:
remains under the radical:
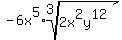 Divide index 3 into 12, the exponent of y
4
3)12
12
0
The quotient is 4 and the remainder is 0
The quotient tells us what power of y comes out of the
radical and the remainder tells us what power of y remains
under the radical. So
Divide index 3 into 12, the exponent of y
4
3)12
12
0
The quotient is 4 and the remainder is 0
The quotient tells us what power of y comes out of the
radical and the remainder tells us what power of y remains
under the radical. So 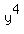 comes out in front of the
radical and no power of y remains under the radical, or
you can say
comes out in front of the
radical and no power of y remains under the radical, or
you can say  which is just 1 remains under the
radical, but we don't even have to write it:
which is just 1 remains under the
radical, but we don't even have to write it:
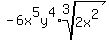 Edwin
Edwin