Question 213034: the square root of 3 over 2 + 3 square roots of one sixth.
show all work please
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! 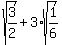
First we'll rationalize the denominator of each term. (In other words we will eliminate the square roots in the denominators.) After that we will see if the square roots can be added together.
The key to rationalizing denominators is to make the denominators perfect squares. The simplest way to do this is to multiply the denominator by itself. Sometimes you can find a smaller number to multiply the denominator by to get a lower perfect square. For example, if you had a denominator that was an 8, you could multiply by 2 giving 16, a perfect square, instead of multiplying by 8. In this problem there are no lower numbers to use so we will multiply each denominator by itself and, of course, we will multiply the numerator by the same number:
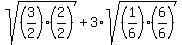
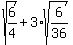
Now we can use the following property,  , to split the numerator and denominator into separate square roots: , to split the numerator and denominator into separate square roots:
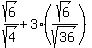
The denominators can now be written as whole numbers:
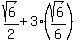
The term on the right can be reduced:

Now, can we add these? When adding with square roots we must have "like" terms. Since both terms have the same square root they are like terms and so they can be added. (It may be helpful to think of the square root as a variable. Let's say  . Then the expression we have is . Then the expression we have is 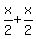 which can be added. This means which can be added. This means 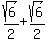 can also be added. can also be added.
Now that we know we can add, how do we add these? First let's rewrite the expression with multiplications instead of divisions:
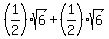
Perhaps now we can see how to add these. In general, half of something plus half of something makes a whole something. (If this is still not clear, think of a variable:  .) So these two halves of the square root of 6 add up to a whole square root of 6!: .) So these two halves of the square root of 6 add up to a whole square root of 6!:

And since this will not simplify any further, we have our answer: 
|
|
|