SOLUTION: Please help me. {{{root(4,5x^8y^3/27x^2)}}}

Subtract the exponents of the 's



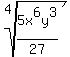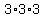Write the   as  and



Now take individual fourth roots of the
top and bottom.




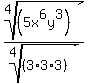The denominator has only three factors of
3.  It needs one more 3, so it will be a 
perfect fourth power, and come out of the
fourth root radical.

So we multiply top and bottom of the fraction
by .



Now that there are 4 factors of 3 in the
denominator, we can write the denominator as
 and simplify the numerator:

 

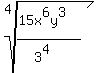Now we take individual fourth roots of the
top and bottom:



And since the bottom is the 4th root of
a 4th power we just take away the 4th root
radical and the 4th power.



The factor 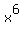 is a case of an exponent 6
under a radical being as large or larger than, in
this case larger than, the index of the radical, 4.
That means it will simplify further.

So we write 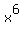 as 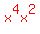 so the 
will come out of the fourth root radical, like the 4
3's did above in the denominator.



Now you can take  out of the radical and
just have  in front of the radical on top:

  

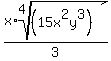Edwin