How do you solve this radical the  ?
?
What I have tried: you isolate the radical to (2x+5)^2 =( x+5)^2
Then I got 5x+25=50 simplify to 5x+50/5 which gave me a final answer of x=5. Am I on the right track?
No. Your first error was a sign error. You got x+5 on the right
and it should have been x-5.
Your second error was in 'squaring a square root'. When
you square  you get just what is under the
radical
you get just what is under the
radical  , not
, not 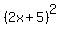 . You don't square what's
under the radical! The squaring takes away BOTH the radical AND
the square, and you get just what's under the radical in the
fourth step.
. You don't square what's
under the radical! The squaring takes away BOTH the radical AND
the square, and you get just what's under the radical in the
fourth step.








 ,
, 
 ,
,  But we must check both solutions in the
original equations:
checking
But we must check both solutions in the
original equations:
checking 





 That checks, so
That checks, so  is a solution:
checking
is a solution:
checking 





 That doesn't check, so the only solution
is
That doesn't check, so the only solution
is
 Edwin
Edwin