SOLUTION: Please help me solve this equation: 2x= 5x+9. The 5x+9 is in a square root. Thank you

Algebra ->  Radicals -> SOLUTION: Please help me solve this equation: 2x= 5x+9. The 5x+9 is in a square root. Thank you      Log On


   

Question 170395: Please help me solve this equation: 2x= 5x+9. The 5x+9 is in a square root.

Thank you
Found 2 solutions by checkley77, Electrified_Levi:
Answer by checkley77(12844) About Me  (Show Source):
You can put this solution on YOUR website!
2x=sqrt(5x+9)
squaring both sides we get:
4x^2=5x+9
4x^2-5x-9=0
(4x-9)(x+1)=0
4x-9=0
4x=9
x=9/4=2.25 ans.
x+1=0
x=-1 ans.
Proofs:
2*2.25=sqrt(5*2.25+9)
4.50=sqrt(11.25+9)
4.5=sqrt(20.25)
4.5=4.5
2*-1=sqrt(5*-1+9)
-2=sqrt(-5+9)
-2=sqrt(4)
-2=+-2

Answer by Electrified_Levi(103) About Me  (Show Source):
You can put this solution on YOUR website!
Hi, Hope I can help,
.
Please help me solve this equation:+2x=sqrt%28+5x%2B9%29+. The 5x+9 is in a square root.
.
Thank you
.
To get rid of the square root sign(radical sign), you square both sides
.
+2x=sqrt%28+5x%2B9%29+ = +%282x%29%5E2=%28sqrt%28+5x%2B9%29%29%5E2+, when you square a number in a square root, it will always be the number inside the sign
.
Ex. ( 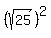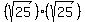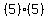+%28sqrt%2825%29%29%5E2+ = +%28sqrt%2825%29%29%28sqrt%2825%29%29+ = +%285%29%285%29+ = +25+
.
So, for our problem, the radical sign disappears if we square both sides
.
+%282x%29%5E2=%28sqrt%28+5x%2B9%29%29%5E2+ = +4x%5E2=+5x%2B9+, now we need to move "5x+9" to the left side
.
+4x%5E2=+5x%2B9+ = +4x%5E2-5x-9=+5x-5x%2B9-9+ = +4x%5E2-5x-9=+0+, this is a quadratic equation
.
Quadratic equations are in the form +ax%5E2%2Bbx%2Bc=+0+, We can solve this equation by using the quadratic equation
.
Quadratic equation = ++%28-b+%2B-+sqrt%28+b%5E2-4%2Aa%2Ac+%29%29%2F%282%2Aa%29+
.
+4x%5E2-5x-9=+0+
.
+ax%5E2%2Bbx%2Bc=+0+
.
For our equation
.
a = 4
.
b = (-5)
.
c = (-9)
.
Now replace the letters with these numbers in the equation
.
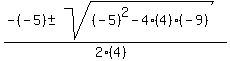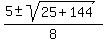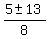
++%28-b+%2B-+sqrt%28+b%5E2-4%2Aa%2Ac+%29%29%2F%282%2Aa%29+ = ++%28-%28-5%29+%2B-+sqrt%28+%28-5%29%5E2-4%2A%284%29%2A%28-9%29+%29%29%2F%282%2A%284%29%29+ = ++%285+%2B-+sqrt%28+25-%28-144%29+%29%29%2F8+ = ++%285+%2B-+sqrt%28+25%2B144+%29%29%2F8+ = ++%285+%2B-+sqrt%28+169+%29%29%2F8+ = ++%285+%2B-+13%29%2F8+
.
+x+=++%285+%2B+13%29%2F8+ = +x+=+18%2F8+ = +x+=+9%2F4+
.
+x+=++%285+-+13%29%2F8+ = +x+=++-8%2F8+ = +x+=+%28-1%29+
.
+x+=+9%2F4+ and +x+=+%28-1%29+, we can check by replacing "x" with these two numbers in the original quadratic equation
.
+x+=+9%2F4+, +4x%5E2-5x-9=+0+ = +4%289%2F4%29%5E2-5%289%2F4%29-9=+0+ = +%284%2F1%29%2881%2F16%29-%285%2F1%29%289%2F4%29-9=+0+ = +%28324%2F16%29-%2845%2F4%29-9=+0+ = +%2881%2F4%29-%2845%2F4%29-9=+0+ = +%2836%2F4%29-9=+0+ = +9+-+9+=+0+ = +0+=+0+ (True)
.
+x+=+%28-1%29+, +4x%5E2-5x-9=+0+ = +4%28-1%29%5E2-5%28-1%29-9=+0+ = +4%281%29-%28-5%29-9=+0+ = +4%2B5-9=+0+ = +9+-+9+=+0+ = +0+=+0+ (True)
.
Since this was not our very first original equation, we have to make sure that the number inside the radical, is not negative, and make sure that the statement is correct
.
+x+=+9%2F4+, +2x=sqrt%28+5x%2B9%29+ = +2%289%2F4%29=sqrt%28+5%289%2F4%29%2B9%29+ = +18%2F4=sqrt%28+%2845%2F4%29%2B9%29+ = +9%2F2=sqrt%28+%2845%2F4%29%2B%2836%2F4%29%29+ = +9%2F2=sqrt%28+%2881%2F4%29%29+ = +9%2F2=9%2F2+ (True)
.
+x+=+%28-1%29+, +2x=sqrt%28+5x%2B9%29+ = +2%28-1%29=sqrt%28+5%28-1%29%2B9%29+ = +%28-2%29=sqrt%28+%28-5%29%2B9%29+ = +%28-2%29=sqrt%28+4%29+ = +%28-2%29+=+2+ (False), +x+=+%28-1%29+ is not an answer
.
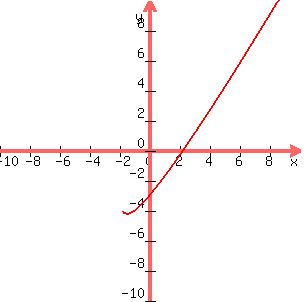
+graph+%28300%2C300%2C-10%2C10%2C-10%2C10%2C+2x+-+sqrt%28+5x%2B9%29%29+
.
The line only crosses at one point on the x axis, at point (9%2F4,0)
.
+x+=+9%2F4+ is your answer
.
Hope I helped, Levi