SOLUTION: [SQRT(x + 7)] - 2[SQRT(x)] =-2 I know x = 9 but I am not sure how to get there. How tall is a stack of cube-shaped blocks whose volumes are 375 cubic inches, 648 cubic inches

Algebra ->  Radicals -> SOLUTION: [SQRT(x + 7)] - 2[SQRT(x)] =-2 I know x = 9 but I am not sure how to get there. How tall is a stack of cube-shaped blocks whose volumes are 375 cubic inches, 648 cubic inches       Log On


   

Question 168292: [SQRT(x + 7)] - 2[SQRT(x)] =-2
I know x = 9
but I am not sure how to get there.
How tall is a stack of cube-shaped blocks whose volumes are 375 cubic inches, 648 cubic inches and 1,029 cubic inches?
A. 10 cubert(3)
B. 6 cubert(3)
C. 3 sqrt(3)
D. 4 sqrt(3)
E. 9 sqt(3)
F. 18 cubert(3)
Answer by Alan3354(69443) About Me  (Show Source):
You can put this solution on YOUR website!
[SQRT(x + 7)] - 2[SQRT(x)] =-2
I know x = 9
--------------
The simplest way is to get one radical by itself, then square both sides.
[SQRT(x + 7)] - 2[SQRT(x)] =-2
sqrt%28x%2B7%29+=+2sqrt%28x%29+-+2
Now square
x%2B7+=+4x+-8sqrt%28x%29+%2B+4
Now isolate the other radical
-8sqrt%28x%29+=+-3x+%2B+3
Square again
64x+=+9x%5E2+-+18x+%2B+9
9x%5E2+-+82x+%2B+9+=+0
Solved by pluggable solver: SOLVE quadratic equation (work shown, graph etc)
Quadratic equation ax%5E2%2Bbx%2Bc=0 (in our case 9x%5E2%2B-82x%2B9+=+0) has the following solutons:

x%5B12%5D+=+%28b%2B-sqrt%28+b%5E2-4ac+%29%29%2F2%5Ca

For these solutions to exist, the discriminant b%5E2-4ac should not be a negative number.

First, we need to compute the discriminant b%5E2-4ac: b%5E2-4ac=%28-82%29%5E2-4%2A9%2A9=6400.

Discriminant d=6400 is greater than zero. That means that there are two solutions: +x%5B12%5D+=+%28--82%2B-sqrt%28+6400+%29%29%2F2%5Ca.

x%5B1%5D+=+%28-%28-82%29%2Bsqrt%28+6400+%29%29%2F2%5C9+=+9
x%5B2%5D+=+%28-%28-82%29-sqrt%28+6400+%29%29%2F2%5C9+=+0.111111111111111

Quadratic expression 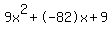9x%5E2%2B-82x%2B9 can be factored:
9x%5E2%2B-82x%2B9+=+%28x-9%29%2A%28x-0.111111111111111%29
Again, the answer is: 9, 0.111111111111111. Here's your graph:
graph%28+500%2C+500%2C+-10%2C+10%2C+-20%2C+20%2C+9%2Ax%5E2%2B-82%2Ax%2B9+%29

The onsite solver doesn't do factors correctly if the coefficient of the the x^2 is not 1, but the answers are right, 9 and 1/9.
---------------------------------------
How tall is a stack of cube-shaped blocks whose volumes are 375 cubic inches, 648 cubic inches and 1,029 cubic inches?
A. 10 cubert(3)
B. 6 cubert(3)
C. 3 sqrt(3)
D. 4 sqrt(3)
E. 9 sqt(3)
F. 18 cubert(3)
-------------------
I don't know what you mean by that. More info is needed.