Question 157288This question is from textbook elementary and intermediate algebra
: How do I find the discriminant? The question ask to find  and the number of real solutions to each equation. and the number of real solutions to each equation.
35. 
45.  This question is from textbook elementary and intermediate algebra
This question is from textbook elementary and intermediate algebra
Found 2 solutions by Edwin McCravy, SAT Math Tutor:
Answer by Edwin McCravy(20054)   (Show Source): (Show Source):
You can put this solution on YOUR website! How do I find the discriminant? The question ask to find  and the number of real solutions to each equation. and the number of real solutions to each equation.
35. 
45. 
You must first rearrange the equations so that 0 appears
on the right and the three terms on the left are in
descending order like this:
 , ,  or whatever
the letter of the unknown happens to be:
That's the only way you can tell what to substitute for or whatever
the letter of the unknown happens to be:
That's the only way you can tell what to substitute for
 , ,  , and , and  in the formula: in the formula:
 -------
For your problem 35:
-------
For your problem 35:
 You must first get a 0 on the right side by adding
You must first get a 0 on the right side by adding 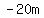 to
both sides: to
both sides:

 And you must write the left side in descending order, like
this:
And you must write the left side in descending order, like
this:
 Then when you compare that to
Then when you compare that to
 ,
it is easy to see that ,
it is easy to see that  , , , and , and  .
So then you can easily substitute those values in the
expression for the discriminant: .
So then you can easily substitute those values in the
expression for the discriminant:



 When the discriminant is 0, there is
exactly 1 real solution. So this particular
quadratic equation has 1 real solution.
If it were negative there would be no real solutions,
and if it were positive there would be exactly two real
solutions.
---------------------------------
For your problem 45:
When the discriminant is 0, there is
exactly 1 real solution. So this particular
quadratic equation has 1 real solution.
If it were negative there would be no real solutions,
and if it were positive there would be exactly two real
solutions.
---------------------------------
For your problem 45:
 You must first get a 0 on the right side by adding
You must first get a 0 on the right side by adding  to
both sides: to
both sides:

 But the left side contains only two terms! So you must
add on a
But the left side contains only two terms! So you must
add on a  to the left side: to the left side:
 Also it may be helpful to write the understood
Also it may be helpful to write the understood  's before 's before
 and and  , like this: , like this:
 The left side is already in descending order, so when you
compare that to
The left side is already in descending order, so when you
compare that to
 ,
it is easy to see that ,
it is easy to see that  , , , and , and  .
So then you can easily substitute those values in the
expression for the discriminant: .
So then you can easily substitute those values in the
expression for the discriminant:



 Since the discriminant is a positive number,
there are exactly two real solutions.
Edwin
Since the discriminant is a positive number,
there are exactly two real solutions.
Edwin
Answer by SAT Math Tutor(36)   (Show Source): (Show Source):
You can put this solution on YOUR website! Begin by setting up a quadratic equation equal to zero so:
35. 4m^2 - 20m + 25 = 0
45. x^2 - x = 0
Then, label a, b, and c which are the coefficients:
35. a = 4, b = -20, c = 25
45. a = 1, b = -1, c = 0
Then, use the discriminant formula b^2 - 4ac:
35. (-20)^2 - 4(4)(25) = 0
45. 1^2 - 4(1)(0) = 1
|
|
|