Question 156831: I need to find x, AB, and BC, where A, B, and C are points on a line...A is the leftmost point, C is the rightmost point, and B is in between A and C (not necessarily the midway)
AB = square root (3x +4)
BC = x-6
AC = 6
I was able to write out sqrt(3x+4) + x - 6 = 6, then simplifies to SQRT (3x+4) + x = 12. I don't understand how to eliminate the square root in these radical equations.
Please help.
Thank you.
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website!
 Start with the given equation. Start with the given equation.
 Add 6 to both sides. Add 6 to both sides.
 Subtract "x" from both sides. Subtract "x" from both sides.
 Square both sides to eliminate the square root Square both sides to eliminate the square root
 FOIL FOIL
 Subtract Subtract  from both sides. Subtract from both sides. Subtract  from both sides. from both sides.
 Combine like terms. Combine like terms.
Notice we have a quadratic equation in the form of  where where  , ,  , and , and 
Let's use the quadratic formula to solve for x
 Start with the quadratic formula Start with the quadratic formula
 Plug in Plug in  , ,  , and , and 
 Negate Negate  to get to get  . .
 Square Square  to get to get 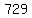 . .
 Multiply Multiply 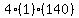 to get to get 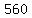
 Subtract Subtract 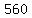 from from 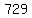 to get to get 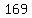
 Multiply Multiply  and and  to get to get  . .
 Take the square root of Take the square root of 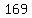 to get to get  . .
 or or  Break up the expression. Break up the expression.
 or or  Combine like terms. Combine like terms.
 or or  Simplify. Simplify.
So the possible answers are  or or 
However, if you plug  back into the original equation, you'll find that it doesn't work. back into the original equation, you'll find that it doesn't work.
So the only solution is 
Now plug in  into AB, BC, and AC into AB, BC, and AC



So the lengths are  , ,  , and , and 
Check:
Remember, AB+BC=AC
AB+BC=AC ... Start with the given equation
5+1=6 ... Plug in  , ,  , and , and 
6=6 ... Add Since this equation is true, this verifies the answer.
|
|
|