Question 15351: 1. Write an equation in the form y=ax^2+bx+c for the quadratic function whose graph passes through (8,0),(0,8) and (-2,0).
2. Find the roots of x^2 + (k^2+1 over k)x+1=0.
3. If (2 over x - x over 2)^2=o,evaluate x^6.
4. Find all values of k that ensure that the roots are real for x-k(x-1)(x-2)=o.
5. Find all possible values of k so that 3x^2 + kx +5 can be factored as the product of two binomial factors with integer cefficients.
6. Show that there are nine pairs of positive integers (m,n) such that m^2+3mn+2n^2-10m-20n=0.
7. The difference in the length of the hypotenuse of triangleABC and the length of the hypotenuse of triangleXYZ is 3. Hypotenuse AB=x,hypotenuse XY=square root x-1 and AB>XY. Determine the length of each hypotenuse.
Answer by khwang(438)   (Show Source): (Show Source):
You can put this solution on YOUR website! You posted so many questions without showing any work,
I don't quite feel happy to solve for you.
1. Write an equation in the form y=ax^2+bx+c for the quadratic function whose graph passes through (8,0),(0,8) and (-2,0).
Sol: Clearly, c = 8, then solve
0 = 64a + 8b + 8 (or 8a + b = -1) and
0 = 4a – 2b (or b = 2a)
for a and b = ???
2.Find the roots of 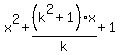 =0. =0.
Sol: Use the quadratic formula directly.
3. If (2 /x – x/ 2)^2 = 0,evaluate x^6.
Sol 2 /x – x/ 2 = 0, so (4-x^2) /2x= 0,
or x = (+/-) 2, Now x^6 = ???
4. Find all values of k that ensure that the roots are real for x-k(x-1)(x-2)=o.
Sol: Convert it to 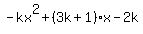 = 0 or = 0 or
 = 0 = 0
Since if  , ,
the given equation has only real roots
Implying  , or , or  . .
Hence,  or or

5. Find all possible values of k so that 3x^2 + kx +5 can be factored as the product of two binomial factors with integer coefficients.
Sol: 3x^2 + kx +5 = (3x+1)(x+5) or (3x-1)(x-5) or (3x+5)(x+1) or (3x-5)(x-1).
Hence, k = ????
6. Show that there are nine pairs of positive integers (m,n) such that

Sol: 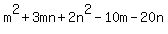 = (m + n)(m + 2n) –10(m+2n) = (m + n)(m + 2n) –10(m+2n)
= (m + 2n) (m+n-10). = 0.
Hence, m + 2n = 0 (no positive sol.)
Or m + n = 10, so there are 9 solutions
{(1,9)(2,8),(3,7),(4,6),(5,5),(6,4),(3,7),(2,8)(1,9)}
7. The difference in the length of the hypotenuse of triangle ABC and the length of the hypotenuse of triangle XYZ is 3. Hypotenuse AB=x, hypotenuse XY= square root x-1 and AB>XY. Determine the length of each hypotenuse.
Sol: Solve the equation x – sqrt(x-1) = 3 or x-3 = sqrt(x-1)
So, (x-3)^2 = x –1 to get x^2-7x +10 = 0 and x = 2 or –5.(invalid)
Bad notation:1. Never use "over" in fraction again.
2. Square root x-1 means ????
You should work very hard.
Kenny
|
|
|