Question 144248: __2____
√[3] + √[2]
Rationalize the demominator?
Answer by solver91311(24713)   (Show Source):
You can put this solution on YOUR website! 
Rationalize the denominator means that you have to get the radical signs out of the denominator. When you have a sum in the denominator where one or both of the terms contain radicals, you can use what you learned about the difference of two squares factorization to find an appropriate multiplier.
Remember that: 
So if you let  , and  , then you know that:
Very nice, except that you can't just multiply the denominator of a fraction by something other than 1 without changing the value of the fraction. You have to multiply the entire fraction by 1. Fortunately, the number 1 comes in many forms because we know that any number divided by itself is 1, in other words,  no matter what  is.
So let's express the number 1 like this  , and multiply this expression by your original fraction:
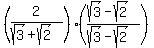
We already know what happens to the denominator, so:
In short, you can define "Rationalize the Denominator" as "Get that pesky radical out of my denominator no matter what kind of mess you make in the numerator"
|
|
|
