Question 143637: How long is a guy wire reaching from the top of a 18 ft pole to a point on the ground 12 feet from the pole?
what is the exact length in feet?
what is the length approximated to three decimal places? round to the nearest thousandths. Thank you so much...
Answer by solver91311(24713)   (Show Source):
You can put this solution on YOUR website! You cannot answer the first part of your question, and it is inappropriate to express your answer to the precision required by the second part of your question. That is because the calculation is based on measurement. No matter how precise a measurement device used, no one can say that the pole is EXACTLY 18 feet tall. In fact, saying that you have an 18 foot pole, expressed as it is to the nearest foot, only guarantees that the true measurement is in the interval [17.5,18.5). And that is why you can't answer the first part and why it would be wrong to answer the second part the way it is requested.
Having said all of that, if you have a right triangle with legs of 18 and 12, you would use the Pythagorean Theorem to determine that the length of the hypotenuse is  . You can then use your calculator to determine 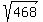 and round off to 3 decimal places. By the way, this solution presumes that the pole is erected on a perfect vertical and the ground is perfectly level such that the pole and the ground form a right angle. Of course, making these assumptions about physical objects, just like assuming that the length is exactly 18 feet and the guy wire is attached exactly 12 feet from the base of the pole, is ludicrous.
|
|
|
