SOLUTION: I have another radical problem. I am just not getting these at all. I feel the veins popping out in my forehead! I have to simplifiy the following problem. 2x divided by the fourth

Algebra ->  Radicals -> SOLUTION: I have another radical problem. I am just not getting these at all. I feel the veins popping out in my forehead! I have to simplifiy the following problem. 2x divided by the fourth      Log On


   

Question 142298: I have another radical problem. I am just not getting these at all. I feel the veins popping out in my forehead! I have to simplifiy the following problem. 2x divided by the fourth root of 3xy^2
Answer by rapaljer(4671) About Me  (Show Source):
You can put this solution on YOUR website!
You must be taking College Algebra!! This one will make the veins pop out in your head!! Take two aspirin and call me in the morning!! Dr. Rapalje

Seriously, if you have a FOURTH ROOT, you need to rationalize the denominators by making the denominators perfect FOURTH POWERS. This means you need to end up in the denominator with numbers like 2^4=16 or 3^4=81. Also, if there are variables, you need to end up with x^4, x^8, x^12, or y^4, y^8, y^12, etc.

Your problem is 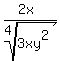%282x%29%2Froot%284%2C3xy%5E2%29+

Since the denominator has a 3, you need to end up with a factor of 81. To do that, you must multiply numerator and denominator by 27. Since you have an x factor, you need to get that up to x^4, so multiply by x^3 over x^3. Since you have a y^2, it will take another y^2 to get it up to y^4. Here is what it looks like:

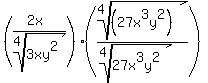
%28%282x%29%2Aroot%284%2C%2827x%5E3y%5E2%29+%29%29%2F%28root%284%2C81x%5E4y%5E4%29+%29+%29+
%282x%2Aroot%284%2C%2827x%5E3y%5E2%29+%29%29%2F%283xy%29++

Finally, reduce the fraction by dividing out the x:
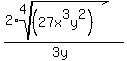
%282%2Aroot%284%2C%2827x%5E3y%5E2%29+%29%29%2F%283y%29++

The best place to look for help with this topic on my own website is to click on my tutor name "rapaljer" anywhere in algebra.com. However, you will need to find my MATH IN LIVING COLOR page (it's easy to find, because it is in LIVING COLOR!), click on College Algebra, and look for "Section 1.06 Rationalizing Monomial Denominators." There are a LOT of easier examples (LIKE this problem but easier!), and they are solved IN COLOR!!
R^2