SOLUTION: How would you solve the problem i^7+i^2+i^12+i^9 over (1-i)^2?

Algebra ->  Radicals -> SOLUTION: How would you solve the problem i^7+i^2+i^12+i^9 over (1-i)^2?      Log On


   

Question 134532: How would you solve the problem i^7+i^2+i^12+i^9 over (1-i)^2?
Found 2 solutions by Earlsdon, josmiceli:
Answer by Earlsdon(6294) About Me  (Show Source):
You can put this solution on YOUR website!
First, it would be helpful to have a table of values for i%5En. You can do this quite easily:
i%5E0+=+1
i%5E1+=+i
i%5E2+=+-1 because i%5E2+=+%28sqrt%28-1%29%29%28sqrt%28-1%29%29= sqrt%28-1%29%5E2+=+-1
i%5E3+=+-i
i%5E4+=+1
i%5E5+=+i
i%5E6+=+-1
i%5E7+=+-i
i%5E8+=+1
i%5E9+=+i
Do you see the pattern?
Simplify:
=0%2F%281-i%29%5E2+=+0

Answer by josmiceli(19441) About Me  (Show Source):
You can put this solution on YOUR website!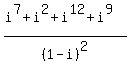
%28i%5E7%2Bi%5E2%2Bi%5E12%2Bi%5E9%29+%2F+%281-i%29%5E2
Note that
i%5E1+=+i
i%5E2+=+-1
i%5E3+=+-1%2Ai
i%5E4+=+-1%2A-1
i%5E5+=+-1%2A-1%2Ai
i%5E6+=+-1%2A-1%2A-1
i%5E7+=+-1%2A-1%2A-1%2Ai
i%5E8+=+-1%2A-1%2A-1%2A-1
So, the sequence is
i, -1, -i, 1, i, -1, -i, 1
If the exponent is 1,5,9,13. . . every other odd #, then
i%5En+=+i
If the exponent is 3,7,11,15 . . .every other odd #, then
i%5En+=+-i
If the exponent is 2,6,10,14 . . .every other even #, then
i%5En+=+-1
If the exponent is 4,8,12,16 . . .every other even #, then
i%5En+=+1
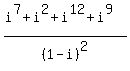
%28i%5E7+%2B+i%5E2+%2B+i%5E12+%2B+i%5E9%29+%2F+%281-i%29%5E2
%28-i+%2B+%28-1%29+%2B+1+%2B+i%29+%2F+%281+-2i+%2B+%28-1%29%29
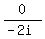
0+%2F+%28-2i%29
Unless I goofed, the answer is 0