Question 1209873: Find all x such that
sqrt{3x^2 + 2x + 1} + sqrt{3x^2 + 2x - 3} = 20.
Found 2 solutions by CPhill, ikleyn:
Answer by CPhill(2138)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let $y = 3x^2 + 2x$. Then the given equation becomes
$$\sqrt{y+1} + \sqrt{y-3} = 20.$$
Isolating one of the square roots, we have
$$\sqrt{y+1} = 20 - \sqrt{y-3}.$$
Squaring both sides, we get
$$y+1 = 400 - 40\sqrt{y-3} + y-3.$$
Simplifying, we have
$$y+1 = 397 + y - 40\sqrt{y-3}.$$
$$40\sqrt{y-3} = 396.$$
Dividing by 40, we get
$$\sqrt{y-3} = \frac{396}{40} = \frac{99}{10} = 9.9.$$
Squaring both sides, we have
$$y-3 = 98.01.$$
$$y = 101.01.$$
Substituting back, we have
$$3x^2 + 2x = 101.01.$$
$$3x^2 + 2x - 101.01 = 0.$$
We can use the quadratic formula to solve for $x$.
$$x = \frac{-2 \pm \sqrt{2^2 - 4(3)(-101.01)}}{2(3)} = \frac{-2 \pm \sqrt{4 + 1212.12}}{6} = \frac{-2 \pm \sqrt{1216.12}}{6}.$$
$$x = \frac{-2 \pm \sqrt{1216.12}}{6} \approx \frac{-2 \pm 34.873}{6}.$$
Therefore,
$$x_1 = \frac{-2 + 34.873}{6} \approx \frac{32.873}{6} \approx 5.4788$$
and
$$x_2 = \frac{-2 - 34.873}{6} \approx \frac{-36.873}{6} \approx -6.1455.$$
Let's check the solutions:
If $x = 5.4788$, then $y = 3x^2 + 2x \approx 3(5.4788)^2 + 2(5.4788) \approx 90.02 + 10.9576 \approx 101.01$.
If $x = -6.1455$, then $y = 3x^2 + 2x \approx 3(-6.1455)^2 + 2(-6.1455) \approx 113.36 - 12.291 \approx 101.01$.
Therefore the solutions are $x \approx 5.4788$ and $x \approx -6.1455$.
Final Answer: The final answer is $\boxed{5.4788, -6.1455}$
Answer by ikleyn(53427)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Find all x such that
sqrt{3x^2 + 2x + 1} + sqrt{3x^2 + 2x - 3} = 20.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Let u = 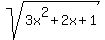 , v = , v =  are new variables.
Then for new variables we have this system of equations
u + v = 20, (1)
u^2 - v^2 = 4 (2)
We can re-write equation (2) this way
(u+v)*(u-v) = 4.
Now replace (u+v) by 20 in this equation, based on (1). You will get
20(u-v) - 4, or u - v = 4/20 = 0.2.
Thus the system (1), (2) takes the form
u + v = 20, (1')
u - v = 0.2 (2')
The solution to (1'), (2') can be found mentally
u = 10.1 (half the sum of 20 and 0.2) and v = 9.9 (half the difference of 20 and 0.2)
From here, we get with the first square root are new variables.
Then for new variables we have this system of equations
u + v = 20, (1)
u^2 - v^2 = 4 (2)
We can re-write equation (2) this way
(u+v)*(u-v) = 4.
Now replace (u+v) by 20 in this equation, based on (1). You will get
20(u-v) - 4, or u - v = 4/20 = 0.2.
Thus the system (1), (2) takes the form
u + v = 20, (1')
u - v = 0.2 (2')
The solution to (1'), (2') can be found mentally
u = 10.1 (half the sum of 20 and 0.2) and v = 9.9 (half the difference of 20 and 0.2)
From here, we get with the first square root
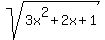 = 10.1,
3x^2 + 2x + 1 = = 10.1,
3x^2 + 2x + 1 = 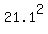 = 102.01,
3x^2 + 2x - 101.01 = 0, = 102.01,
3x^2 + 2x - 101.01 = 0,
 = =  = 5.47882..., = 5.47882...,
 = = 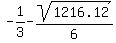 = -6.14549... using the quadratic formula.
With the second square root we get = -6.14549... using the quadratic formula.
With the second square root we get
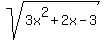 = 9.9,
3x^2 + 2x - 3 = = 9.9,
3x^2 + 2x - 3 = 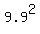 = 98.01,
3x^2 + 2x - 101.01 = 0,
It is the same equation as above, so it does not add additional roots.
So, there are 2 approximate solutions : -6.14549 and 5.47882. ANSWER = 98.01,
3x^2 + 2x - 101.01 = 0,
It is the same equation as above, so it does not add additional roots.
So, there are 2 approximate solutions : -6.14549 and 5.47882. ANSWER
Solved.
|
|
|