SOLUTION: Find the real solutions of the equation. x^2 + 3x + sqrt{x^2 + 3x} = 6 I was to able reduce it to look like this: x^2 + 3x = (x^2 + 3x - 6)^4 Stuck here ....

    x^2 + 3x + 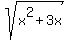 = 6.    (1)


It is a standard equation to solve using "change of a variable".


So, we introduce new variable  y = .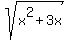


Then equation (1) takes the form

    y^2 + y = 6,

or

    y^2 + y - 6 = 0.


We look for non-negative solutions of this equation.


Factor left side

    (y+3)*(y-2) = 0


and get two roots y= -3  and  y= 2.


For what follows, we consider only positive value y= 2.

The root y= 2  leads  to equation 

    x^2 + 3x = 2^2 = 4,

    x^2 + 3x - 4 = 0,

    (x+4)*(x-1) =  0   with the solutions  x= -4  and x= 1.


Of these two solutions, both work. 


ANSWER.  There are two real solutions for x: they are  x= -4  and  x= 1.