Question 1199216: Solve for x.
x^(3/2) - 3x^(1/2) = 0
sqrt{x^2} - sqrt{3x} = 0
After squaring both sides, I got x^3 = 3x.
x^3 - 3x = 0
x(x^2 - 3) = 0
x = 0 and x^2 - 3 = 0
Solving x^2 - 3 = 0 for x, I got sqrt|3}, -sqrt{3}.
After checking my answers for x, I concludes that the only two solutions
for x are 0 and sqrt{3}.
The textbook answers for x are 0 and 3.
Why am I wrong?
Found 3 solutions by ikleyn, greenestamps, math_tutor2020:
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
You are wrong starting from the third line in your post.
--------------
Comment from student : Why is my third line wrong?
My response : If you ask such questions, it means that you do not know the necessary basics.
In other words, you do not have a necessary prerequisites to solve such problems.
In short, you are in wrong class.
Answer by greenestamps(13200)   (Show Source): (Show Source):
Answer by math_tutor2020(3817)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The 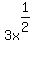 is not the same as is not the same as 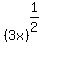
In the first expression, we apply the 1/2 exponent to only the x; while the second expression has the exponent apply to all of 3x.
Recall that with PEMDAS, the parenthesis is done first, then exponents, then multiplication.
P = parenthesis
E = exponents
M = multiplication
D = division
A = addition
S = subtraction
The reason I bring this up is that with 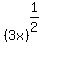 , we compute the 3x first in the parenthesis, then apply the exponent later. , we compute the 3x first in the parenthesis, then apply the exponent later.
Whereas with 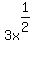 , we do the exponent piece , we do the exponent piece 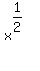 first before multiplying with the 3 out front. first before multiplying with the 3 out front.
-----------------------------
Here is one way to solve for x.

 Rearrange exponents in the first term. Use the rule a^(b*c) = (a^b)^c. Rearrange exponents in the first term. Use the rule a^(b*c) = (a^b)^c.
 Raising to the 1/2 power is the same as a square root. Raising to the 1/2 power is the same as a square root.

 Square both sides Square both sides




 or or  or or 
 or or  or or 
Those are the potential solutions.
But we need to check each of them.
-----------------------------
If you were to plug in x = 0 into the original equation, then,






We end up with a true statement, therefore confirming x = 0 is indeed a root.
-----------------------------
Repeat for x = 3







We have confirmed x = 3 is also a root.
-----------------------------
Now try x = -3



We see that a negative is under the square root, to produce a complex value in the form a+bi, where 
So we'll ignore x = -3.
-----------------------------
Another approach to take is to use a factoring method similar to what @greenestamps mentioned.






 or or 
 or or 
|
|
|