Question 1151181: Given that x and y are integers and
 , , find , , find 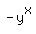
Answer by Edwin McCravy(20066)   (Show Source): (Show Source):
You can put this solution on YOUR website! Your equation is
 , find , find 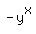 After working on it, I found that there is no solution in integers.
However if the minus sign before the square root on the right side is changed to
plus, there is a solution. I will prove that I am right.
I'll first do it with the minus sign, just as was given, show that there is no
solution, then change that minus sign to plus, and find the solution.
First we simplify the left side by writing it as the sum of two square roots of
integers.
After working on it, I found that there is no solution in integers.
However if the minus sign before the square root on the right side is changed to
plus, there is a solution. I will prove that I am right.
I'll first do it with the minus sign, just as was given, show that there is no
solution, then change that minus sign to plus, and find the solution.
First we simplify the left side by writing it as the sum of two square roots of
integers.
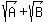 , where A and B are positive integers. , where A and B are positive integers.
 Square both sides:
(1)
Square both sides:
(1)  Equate the terms with square roots:
Equate the terms with square roots:
 Divide both sides by 2
Divide both sides by 2
 Square both sides
Square both sides

 Equate the terms of (1) that do not have square roots:
Equate the terms of (1) that do not have square roots:
 So we have the system of equations:
So we have the system of equations:
 Solve that by substitution and get {A,B} = {11,16}
So the left side of the original equation is
Solve that by substitution and get {A,B} = {11,16}
So the left side of the original equation is
 or
or
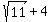 We might stop here to convince ourselves with a calculator
that the left side of the original equation actually does
equal to the above expression.
We might stop here to convince ourselves with a calculator
that the left side of the original equation actually does
equal to the above expression.
 By calculator, we get the same approximation 7.31662479 for both expressions,
so that satisfies us that the left side of the original equation does simplify
to
By calculator, we get the same approximation 7.31662479 for both expressions,
so that satisfies us that the left side of the original equation does simplify
to 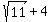 Now the original equation becomes:
Now the original equation becomes:

 Since y is an integer, so is y-4.
Suppose that integer is A. Then
Since y is an integer, so is y-4.
Suppose that integer is A. Then

 Square both sides:
Square both sides:

 Since x, y, and A are all integers the right side is also an integer.
However the left side is not an integer but is irrational.
Therefore I have proved that your equation as stated has no solution.
That's because an integer cannot equal to an irrational number.
However if the original equation had been this:
Since x, y, and A are all integers the right side is also an integer.
However the left side is not an integer but is irrational.
Therefore I have proved that your equation as stated has no solution.
That's because an integer cannot equal to an irrational number.
However if the original equation had been this:
 Then we would have had this:
Then we would have had this:
 The two sides will be exactly the same if y=4 and x-2y=11
Substituting 4 for y in
x-2y=11
x-2(4)=11
x-8=11
x=19
So the solution with the minus changed to plus is x=19, y=4.
Then,
The two sides will be exactly the same if y=4 and x-2y=11
Substituting 4 for y in
x-2y=11
x-2(4)=11
x-8=11
x=19
So the solution with the minus changed to plus is x=19, y=4.
Then,  You should call your teacher's attention to this. It has to be an error.
Edwin
You should call your teacher's attention to this. It has to be an error.
Edwin
|
|
|