Question 113395: Hello out there,I need some help with some really tough problems,I only have two of them,the first one is,Determine whether the number is rational or irrational.If it is irrational,find two consecutive integers between which its graph lies on the number line,-sqrt81.And the last one is,Determine whether sqrt 67 is rational or irrational.If it is irrational,find two consecutive integers between which its graph lies on the number line.Thanks to whoever can help.
Answer by solver91311(24713)   (Show Source): (Show Source):
You can put this solution on YOUR website!  because because  . 9 is clearly a rational number because it can be expressed as the ratio of two integers: . 9 is clearly a rational number because it can be expressed as the ratio of two integers:  for example. for example.
67 is not a perfect square, because  and and  . So, . So, 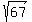 is some number between 8 and 9. But, is it rational or irrational? is some number between 8 and 9. But, is it rational or irrational?
Let's suppose the square root of 67 is a rational number. Then it must be
of the form a/b, where a and b are whole numbers. Furthermore, we can
assume that a and b don't have any common factor (otherwise we could
just divide the numerator and denominator by the common factor).
So we have  , so , so


This means that a squared is a multiple of 67. Now you can easily see
that to get a number that is a multiple of 67 by squaring a, a itself
must be a multiple of 67, so  for some whole number c. Putting for some whole number c. Putting
this back into the equation, we get

Now we divide both sides of the equation by 67, getting

So  is a multiple of 67, and b must be a multiple of 67. is a multiple of 67, and b must be a multiple of 67.
But now we are in trouble, because we have shown that both a and b are
multiples of 67, but we know that a and b have no common factor, since we chose  at the start to be reduced to lowest terms. So at the start to be reduced to lowest terms. So
our original assumption that 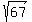 was rational must was rational must
have been wrong. Therefore, 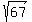 is irrational. is irrational.
Hope this helps,
John
|
|
|