Suppose Jonathan takes x hours to build 1 shed
Then Jonathan's shed-building rate is 1 shed per x hours.
That's  or
or 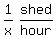
Jonathan and Jose could build a shed, working together, in 6 1/2 hours;
So their combined shed-building rate is 1 shed per 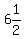 hours.
That's
hours.
That's 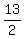 hours
That's
hours
That's  or
or  or
or 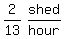 So their combined rate is 2/13:
So their combined rate is 2/13:
but Jonathan worked alone for 3 hours
So using RATE × TIME = PRODUCTION (IN FRACTION OF A FENCE)
 =
= 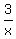 = Jonathon's production as part of a
fence during the first 3 hours.
There was still 1 fence MINUS the part of the fence (3/x) which
Jonathon finished during the first 3 hours. That's the fraction
= Jonathon's production as part of a
fence during the first 3 hours.
There was still 1 fence MINUS the part of the fence (3/x) which
Jonathon finished during the first 3 hours. That's the fraction
 of a fence
left to be built.
of a fence
left to be built.
and was then joined by Jose,
Therefore their rate was the combined rate of 2/13 of a fence per hour.
after which they finished the shed in 5 hours.
So using RATE × TIME = PRODUCTION (IN FRACTION OF A FENCE)





 So Jonathon could build a shed by himself in 13 hours,
so his shed-building rate is
So Jonathon could build a shed by himself in 13 hours,
so his shed-building rate is
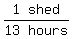 or
or 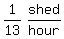 and since he worked a total of 3+5 or 8 hours, the
fraction of the fence Jonathan built was
and since he worked a total of 3+5 or 8 hours, the
fraction of the fence Jonathan built was 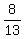 of the fence.
Therefore Jose built the remaining
of the fence.
Therefore Jose built the remaining  of the fence.
of the fence.
If they were paid in proportion to what the amount of work each accomplished, how should $96 be divided between them?
So Jonathon was paid 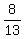 times $96 or $59.08 and
Jose was paid
times $96 or $59.08 and
Jose was paid  times $96 or $36.92.
Edwin
times $96 or $36.92.
Edwin