Question 1107096: Evaluate  +... +...
Found 2 solutions by Edwin McCravy, ikleyn:
Answer by Edwin McCravy(20067)   (Show Source): (Show Source):
Answer by ikleyn(52943)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
I am familiar with this problem . . .
It was posted to the forum a week or two ago, and I solved it . . .
So, I know that the formulation in THIS post IS NOT EXACTLY PRECISE.
Therefore, I edited it, and the EDITED formulation (the only correct, valid and right version) is THIS:
Evaluate 
Below is the solution:
Let us consider, for brewity of writing, more general expression
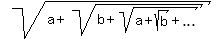 = x, (1)
where a = = x, (1)
where a =  , b = , b =  . Square (1) (both sides). You will get then . Square (1) (both sides). You will get then
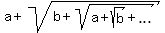 = =  , ,
 = =  . (2)
Square (2) (both sides). You will get then . (2)
Square (2) (both sides). You will get then
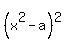 = =  . (3) . (3)
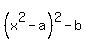 = =  . (4)
Notice that the right side of the expression (4) is the same as the given expression, so it is equal to x. Thus you have . (4)
Notice that the right side of the expression (4) is the same as the given expression, so it is equal to x. Thus you have
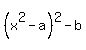 = x.
It is equivalent to = x.
It is equivalent to
 - -  = x, or = x, or
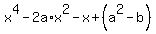 = 0.
Now substitute here a = = 0.
Now substitute here a =  , b = , b =  . You will get this equation in the form . You will get this equation in the form
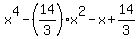 = 0, or, multiplying all the terms by 3 = 0, or, multiplying all the terms by 3
 = 0.
The plot of the last polynomial is shown below. = 0.
The plot of the last polynomial is shown below.
 Plot y =
Plot y = 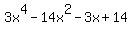 It clearly shows that x= 1 and x= 2 are the roots. Having this HINT, you can check it MANUALLY (as I did . . . ).
The two other roots of the polynomial are complex numbers.
Since the value of
It clearly shows that x= 1 and x= 2 are the roots. Having this HINT, you can check it MANUALLY (as I did . . . ).
The two other roots of the polynomial are complex numbers.
Since the value of 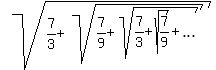 is, obviously, real number greater than 1, it can be only 2.
It proves that is, obviously, real number greater than 1, it can be only 2.
It proves that 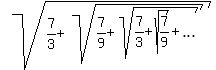 = 2.
Answer. = 2.
Answer. 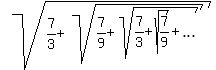 = 2.
Check. = 2.
Check. 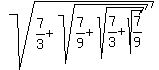 = 1.984 (approximately). = 1.984 (approximately).
---------------
See the lesson
- Evaluating expressions that contain infinitely many square roots
in this site.
|
|
|