Question 1033443: Rationalize the denominator. Simplify, if possible.
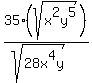
I know that the answer is  , but I'm looking for an in depth explanation on how to get it.
Answer by Boreal(15235)   (Show Source):
You can put this solution on YOUR website! The numerator is 35 xy^2 sqrt(y). Every exponent of 2 under the radical becomes 1, and anything left over stays under the radical.
The denominator is 2x^2(sqrt 7y), because sqrt (28)=sqrt(4)*sqrt(7)
This is 35y^2 /2x sqrt (7), because the sqrt (y) cancels
Multiply top and bottom by sqrt (7) to rationalize
35 y^2 sqrt(7)/2x*7
=5y^2 sqrt (7)/2x
====================
Look at each part of the fraction. Start with the numbers
On top there is 35. On the bottom is the square root of 28, which is square root of 4*square root of 7=2 square root of 7. When there is a square root in the denominator, that has to be multiplied by itself to make it rational (fraction of two integers is a rational number, for example, and square root of 7 cannot be written as the fraction of two integers). This is 35/2 square root (7). If you multiply top and bottom by square root of 7, the bottom has square root of 7* square root of 7=7. That is rational. The numerator now has 35 square root of 7, which is irrational, but it is in the numerator.
35 square root of 7/2*7=(5/2) square root of 7. That is part of the answer, and you can see it. If the other parts are not clear, ask further, and I will go through that.
|
|
|
