SOLUTION: Please help me with the problems below, it would be gladly appreciated. Thank you! <3 Solve the equation using any method. Round to the nearest tenth, if necessary. 1.)

Algebra ->  Radicals -> SOLUTION: Please help me with the problems below, it would be gladly appreciated. Thank you! <3 Solve the equation using any method. Round to the nearest tenth, if necessary. 1.)       Log On


   

Question 1028736: Please help me with the problems below, it would be gladly appreciated. Thank you! <3

Solve the equation using any method. Round to the nearest tenth, if necessary.

1.) x^2-144=0

2.) x^2-6x=-8

3.) 2x^2-5x-13=0

4.) 9x^2+48x=36
Answer by Alan3354(69443) About Me  (Show Source):
You can put this solution on YOUR website!
Solve the equation using any method. Round to the nearest tenth, if necessary.

1.) x^2-144=0
x^2 = 144
x = ± 12
---------------
2.) x^2-6x=-8
x^2 - 6x + 8 = 0
Find a pair of factors of 8 with a sum of -6
=====================
3.) 2x^2-5x-13=0
Solved by pluggable solver: SOLVE quadratic equation (work shown, graph etc)
Quadratic equation ax%5E2%2Bbx%2Bc=0 (in our case 2x%5E2%2B-5x%2B-13+=+0) has the following solutons:

x%5B12%5D+=+%28b%2B-sqrt%28+b%5E2-4ac+%29%29%2F2%5Ca

For these solutions to exist, the discriminant b%5E2-4ac should not be a negative number.

First, we need to compute the discriminant b%5E2-4ac: b%5E2-4ac=%28-5%29%5E2-4%2A2%2A-13=129.

Discriminant d=129 is greater than zero. That means that there are two solutions: +x%5B12%5D+=+%28--5%2B-sqrt%28+129+%29%29%2F2%5Ca.

x%5B1%5D+=+%28-%28-5%29%2Bsqrt%28+129+%29%29%2F2%5C2+=+4.08945417290014
x%5B2%5D+=+%28-%28-5%29-sqrt%28+129+%29%29%2F2%5C2+=+-1.58945417290014

Quadratic expression 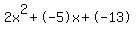2x%5E2%2B-5x%2B-13 can be factored:
2x%5E2%2B-5x%2B-13+=+%28x-4.08945417290014%29%2A%28x--1.58945417290014%29
Again, the answer is: 4.08945417290014, -1.58945417290014. Here's your graph:
graph%28+500%2C+500%2C+-10%2C+10%2C+-20%2C+20%2C+2%2Ax%5E2%2B-5%2Ax%2B-13+%29


-----------------------------------------
4.) 9x^2+48x=36
Divide by 3
3x^2 + 16x - 12 = 0
Solved by pluggable solver: SOLVE quadratic equation (work shown, graph etc)
Quadratic equation ax%5E2%2Bbx%2Bc=0 (in our case 3x%5E2%2B16x%2B-12+=+0) has the following solutons:

x%5B12%5D+=+%28b%2B-sqrt%28+b%5E2-4ac+%29%29%2F2%5Ca

For these solutions to exist, the discriminant b%5E2-4ac should not be a negative number.

First, we need to compute the discriminant b%5E2-4ac: b%5E2-4ac=%2816%29%5E2-4%2A3%2A-12=400.

Discriminant d=400 is greater than zero. That means that there are two solutions: +x%5B12%5D+=+%28-16%2B-sqrt%28+400+%29%29%2F2%5Ca.

x%5B1%5D+=+%28-%2816%29%2Bsqrt%28+400+%29%29%2F2%5C3+=+0.666666666666667
x%5B2%5D+=+%28-%2816%29-sqrt%28+400+%29%29%2F2%5C3+=+-6

Quadratic expression 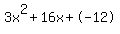3x%5E2%2B16x%2B-12 can be factored:
3x%5E2%2B16x%2B-12+=+%28x-0.666666666666667%29%2A%28x--6%29
Again, the answer is: 0.666666666666667, -6. Here's your graph:
graph%28+500%2C+500%2C+-10%2C+10%2C+-20%2C+20%2C+3%2Ax%5E2%2B16%2Ax%2B-12+%29