Question 1019710: |x|>k is equivalent to?
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! i believe the answer is going to be x < -k and x > k
here's how to figure.
start with abs(x) > k
abs(x) means the same as |x| which means absolute value of x.
so start with abs(x) > k.
now abs(x) is equal to x if x > 0 and abs (x) is equal to -x if x < 0.
therefore:
abs(x) > k can be broken up into two equations, one where x is greater than 0 and one where x is smaller than 0.
you get:
-x > k when x is smaller than 0, and x > k when x is greater than 0.
when x is smaller than 0, the equation of -x > k is solved for x as follows:
start with -x > k
multiply both sides of this equation by -1 to get x < -k.
when you multiply both sides of an inequality by a negative number, the inequality reverses.
so, when x < 0, you get x < -k.
when x is greater than 0, the equation of x > k is solved for x as follows:
start with x > k
you're done since the equation has already been solved.
so you have x < -k or x > k.
in interval notation, this solution would be shown as (-infinity,-k) union (k,infinity).
if you were able to graph this inequality, you would get a graph that looks like this:
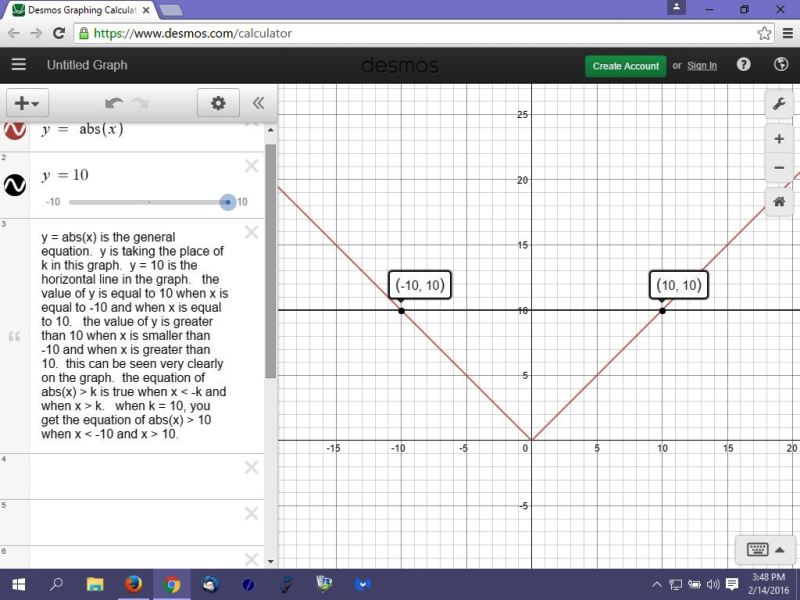
|
|
|