Advanced problems on solving equations containing radicals
Problem 1
Solve an equation  +
+ 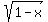 +
+ 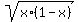 = 1
= 1
Solution
 +
+ 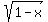 +
+ 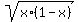 = 1. (1)
The domain, where all included functions are defined, is the segment [0,1].
Two obvious solutions to the given equation in this domain are x= 0 and x= 1.
Below I will show that the given equation HAS NO other solutions.
Indeed, let 0 < x < 1.
Then
= 1. (1)
The domain, where all included functions are defined, is the segment [0,1].
Two obvious solutions to the given equation in this domain are x= 0 and x= 1.
Below I will show that the given equation HAS NO other solutions.
Indeed, let 0 < x < 1.
Then  is defined and is positive number
is defined and is positive number  > 0.
Similarly,
> 0.
Similarly, 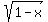 is defined and is positive number
is defined and is positive number 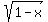 > 0.
For any two real positive numbers "a" and "b" the following inequality is valid
a + b >
> 0.
For any two real positive numbers "a" and "b" the following inequality is valid
a + b > 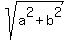 . (2)
To prove it, square both sides. You will get
a^2 + 2ab + b^2 > a^2 + b^2,
which is valid for all positive "a" and "b".
Now apply the inequality (2) for a=
. (2)
To prove it, square both sides. You will get
a^2 + 2ab + b^2 > a^2 + b^2,
which is valid for all positive "a" and "b".
Now apply the inequality (2) for a=  and b=
and b= 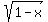 . You will get
. You will get
 +
+ 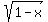 >
> 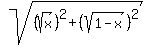 =
= 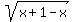 =
= 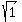 = 1.
Thus, the sum
= 1.
Thus, the sum  +
+ 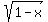 at 0 < x < 1 is just greater than 1.
With the added positive addend
at 0 < x < 1 is just greater than 1.
With the added positive addend 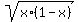 , the sum
, the sum  +
+ 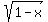 +
+ 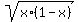 is just even more than 1.
Therefore, the sum
is just even more than 1.
Therefore, the sum  +
+ 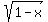 +
+ 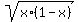 can not be equal to 1 at 0 < x < 1.
Thus, it PROVED that the given equation has no solutions inside the segment [0,1].
So, the endpoints x= 0 and x= 1 are the only solutions.
can not be equal to 1 at 0 < x < 1.
Thus, it PROVED that the given equation has no solutions inside the segment [0,1].
So, the endpoints x= 0 and x= 1 are the only solutions.
Problem 2
Solve an equation 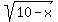 +
+ 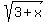 +
+ 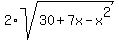 = 17.
= 17.
Solution
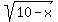 +
+ 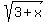 +
+ 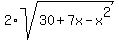 = 17 (1)
= 17 (1)
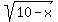 +
+ 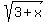 = 17 -
= 17 - 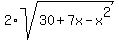 Square both sides
(10-x) +
Square both sides
(10-x) + 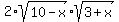 + (3+x) = 17 -
+ (3+x) = 17 - 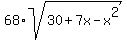 + 4*(30 +7x - x^2)
Notice that (10-x)*(3+x) = 30 + 7x - x^2, and continue transform preceding equations
(10-x) +
+ 4*(30 +7x - x^2)
Notice that (10-x)*(3+x) = 30 + 7x - x^2, and continue transform preceding equations
(10-x) + 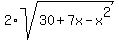 + (3+x) = 289 -
+ (3+x) = 289 - 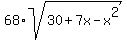 + 4*(30 +7x - x^2)
13 +
+ 4*(30 +7x - x^2)
13 + 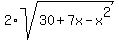 = 289 -
= 289 - 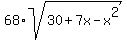 + 4*(30+7x-x^2)
0 = 276 -
+ 4*(30+7x-x^2)
0 = 276 - 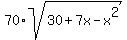 + 4*(30+7x-x^2) (2)
Introduce new variable t =
+ 4*(30+7x-x^2) (2)
Introduce new variable t = 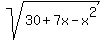 .
Then equation (2) takes the form
4t^2 - 70t + 276 = 0.
Solve it using the quadratic formula
.
Then equation (2) takes the form
4t^2 - 70t + 276 = 0.
Solve it using the quadratic formula
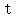 =
= 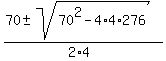 =
= 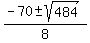 =
= 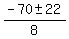 .
Case 1. t =
.
Case 1. t = 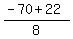 = -6.
Then t =
= -6.
Then t = 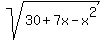 = -6 implies (after squaring both sides)
30 + 7x - x^2 = 36
x^2 - 7x + 6 = 0
(x-1)*(x-6) = 0
The roots are x= 1 and x= 6.
You can easily check that both these roots satisfy the original equation.
Case 2. t =
= -6 implies (after squaring both sides)
30 + 7x - x^2 = 36
x^2 - 7x + 6 = 0
(x-1)*(x-6) = 0
The roots are x= 1 and x= 6.
You can easily check that both these roots satisfy the original equation.
Case 2. t = 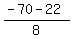 = -11.5.
Then t =
= -11.5.
Then t = 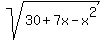 = -11.5 implies (after squaring both sides)
30 + 7x - x^2 = 132.25
x^2 - 7x + 102.25 = 0
Discriminant d = b^2 - 4ac = 7^2 - 4*102.25 is negative,
Hence, this case does not produce real solutions.
The solution is completed.
The ANSWER is: the original equation has two solutions x= 1 and x= 6.
= -11.5 implies (after squaring both sides)
30 + 7x - x^2 = 132.25
x^2 - 7x + 102.25 = 0
Discriminant d = b^2 - 4ac = 7^2 - 4*102.25 is negative,
Hence, this case does not produce real solutions.
The solution is completed.
The ANSWER is: the original equation has two solutions x= 1 and x= 6.
Problem 3
Solve an equation 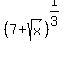 +
+ 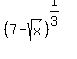 = 2.
= 2.
Solution
Your starting equation is
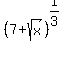 +
+ 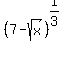 = 2. (1)
Let a =
= 2. (1)
Let a = 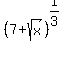 ; b =
; b = 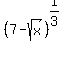 .
Raise both sides of equation (1) to degree 3.
Use
.
Raise both sides of equation (1) to degree 3.
Use
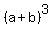 =
=  + 3ab*(a+b),
+ 3ab*(a+b),
 =
= 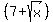 +
+  = 14,
a + b = 2 <<<---=== given by equation,
ab =
= 14,
a + b = 2 <<<---=== given by equation,
ab =  .
You will get
.
You will get
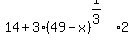 = 8.
Simplify and find x
= 8.
Simplify and find x
 =
= 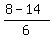 ,
,
 = -1.
Raise both sides of the last equation to degree 3
49 - x = -1,
49 + 1 = x,
x = 50.
ANSWER. x = 50.
CHECK.
= -1.
Raise both sides of the last equation to degree 3
49 - x = -1,
49 + 1 = x,
x = 50.
ANSWER. x = 50.
CHECK. 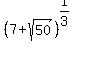 +
+ 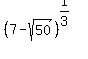 = 2.414213562 + (-0.414213562) = 2.0000000
= 2.414213562 + (-0.414213562) = 2.0000000
My other lesson on solving equations containing radicals is
- HOW TO solve equations containing radicals
- Solving systems of equations containing radicals
- OVERVIEW of my lessons on solving equations containing radicals
in this site.
Use this file/link ALGEBRA-I - YOUR ONLINE TEXTBOOK to navigate over all topics and lessons of the online textbook ALGEBRA-I.

