Question 992302: Hyperbola
Determine the center,vertices, foci,conjugat, and the latus rectum of the
(y+3)^2/16 - (x-2)^2/25=1
Answer by MathLover1(20850)   (Show Source):
You can put this solution on YOUR website!  ....if you compare to  you see that  , ,  ,
since the  part of the equation is added, then the center, foci, and vertices will be above and below the center (on a line paralleling the y-axis)
so,
the center is at ( , )= ( , )
semi-major axis length 
semi-minor axis length 
since  and  , the equation  tells me that  , so  , and
the eccentricity is 
the vertices and foci are above and below the center,
so the foci are at
(, )=(, ) and
(, )= (, )
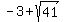or, approximately at (,  ) and (, )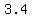
the vertices are at (, ) and (,  )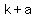
(, ) =>(, )
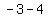and
(,  )=>(, )
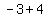The length of the Latus Rectum:
In a hyperbola, it is twice the square of the length of the transverse axis divided by the length of the conjugate axis.
the length of the transverse axis is  => =>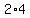
the length of the conjugate axis is  => =>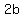
the Latus Rectum is 
|
|
|
