Question 973502: Conics: Equation: 16y^2=49x^2+784
I need all necessary parts and need to know which conic it is
Answer by KMST(5328)   (Show Source):
You can put this solution on YOUR website! 
The original equation can be transformed into an equivalent form
that will make all you need to know very clear.
It so happens that  ,
one of those lucky coincidences that happen very often in math homework.
It is clear from the last equation above that for  ,  .
You can also see that since  ,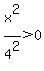
it must be true that  <---> for all the points in the graph.
That means that the horizontal band with 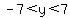 is a forbidden zone that the graph does not enter.
It also means that the points (0,-7), and (0,7) found above are the vertices, and that this is a hyperbola.
<---> <---> <---> also makes it clear that as  increases,
the curve approaches the lines where
 <---> <---> .
Those two straight lines are the asymptotes.
So far we know that the curve looks like this
 ,
a smile and a frown tangent on the oustside to the horizontal lines  ,
all symmetrical with respect to the x-axis and the origin, (0,0).
All that is left to do, is to draw that rectangular box bounded by the lines
, and realize that the half sides, and half diagonals of that box area the  ,  and  that they showed you in formulas in math class,
, and being the numbers that appear squared as denominators in ,
and being the distance from the center, (0,0), to the foci, at (0,-c), and (0,c).
 In the right triangle,  <--> -->
|
|
|
